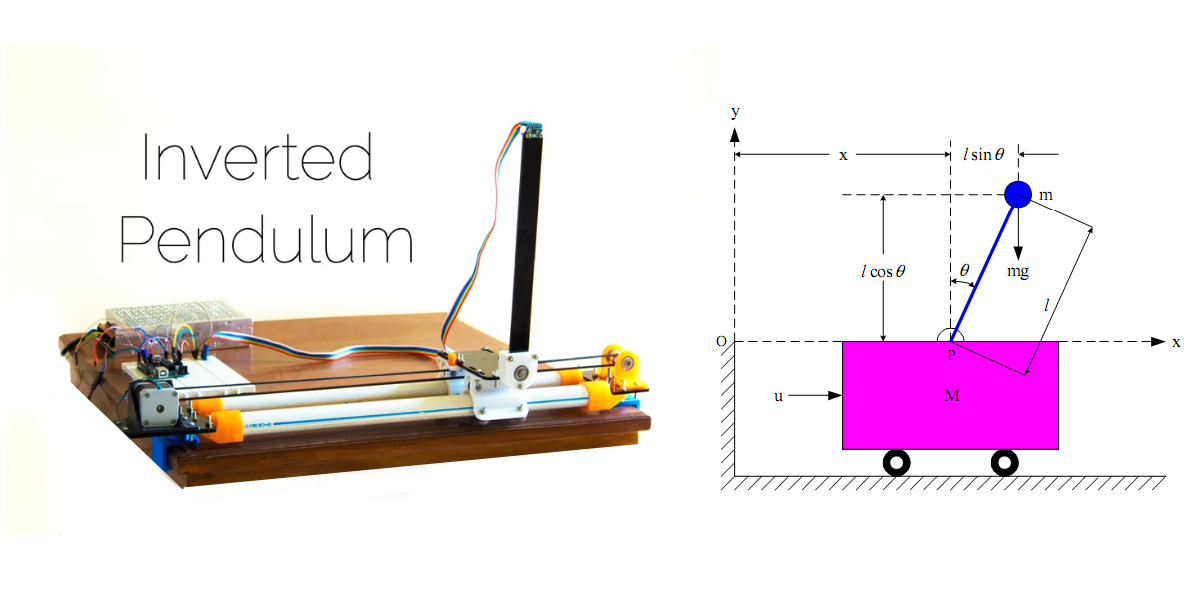
Inverted Pendulum เป็นระบบพลศาสตร์ พื้นฐานสำหรับการศึกษาวิชา Control Systems ในงานชิ้นนี้จะนำเสนอการจำลองการควบคุม Inverted Pendulum เบื้องต้น โดยใช้แบบจำลองที่เป็นเชิงเส้น(Linearization)
Inverted Pendulum สามารถเขียน Free body diagram แยกออกจากกัน 2 ชิ้น ได้ดังนี้
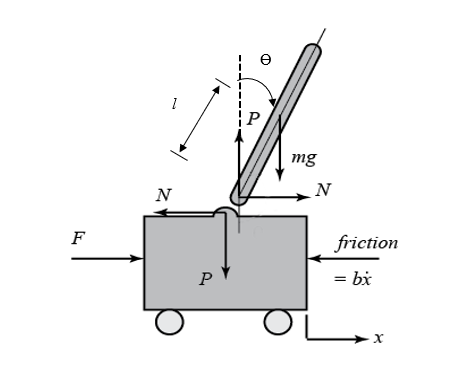
M มวลของรถ (0.7kg)
m มวลของ Pendulum (0.3kg)
b สัมประสิทธิแรงเสียดทาน (0.1 N.m.s)
l ระยะทางจากจุดหมุนถึงศูนย์กลางมวลของ Pendulum (0.17m)
I โมเม้นความเฉื่อยของ Pendulum (0.06 \(kg\cdot m^{2}\))
F แรงที่กระทำต่อรถ (1 N)
g แรงโน้มถ่วงของโลก ( 9.81 \( m\setminus s^{2}\))
x ตำแหน่งของรถ จากการเคลื่อนที่
\(\theta \) มุมของ Pendulum
จาก Free body diagram เราจะได้สมการพลศาสตร์ไม่เชิงเส้นดังนี้
(1)
(2)
สมมติให้การทำงานเกิดขึ้นในย่านแคบๆ จึงทำการเปลี่ยนสมการ (1) และ (2) ให้เป็นสมการเชิงเส้น (linearization) รอบๆ จุดทำงานคือ \(\theta=0 \) และจัดรูปสมการใหม่ จะได้
(3)
(4)
ทำการเปลี่ยน สมการ (3) และ (4) เป็น Simulink control block ได้ดังนี้
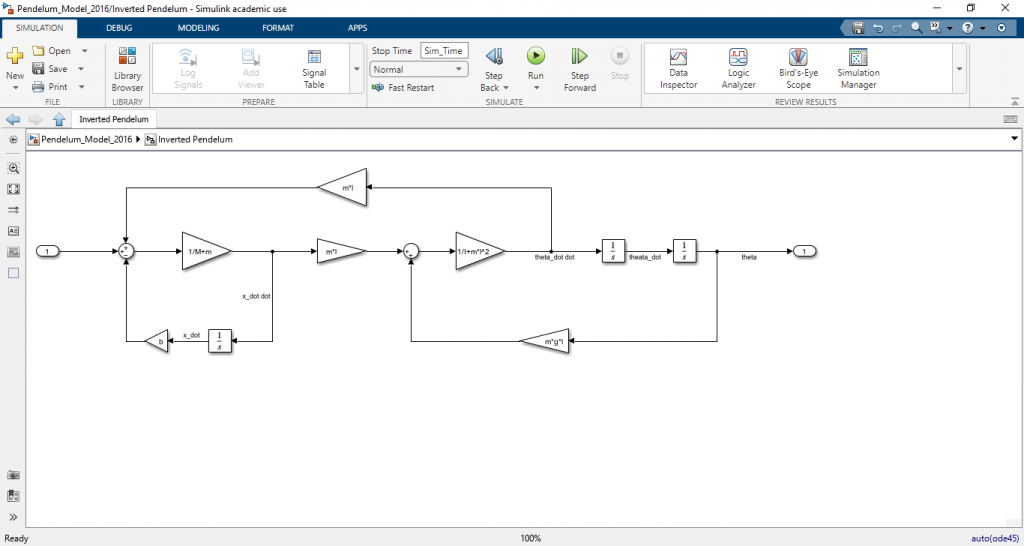
สร้างระบบการควบคุมแบบวงปิด โดยการเพิ่ม PID Controller เข้าไปในระบบ
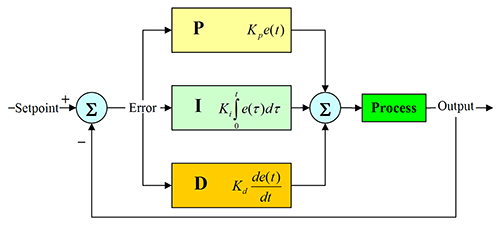
จากไดอะแกรมพีไอดีคอนโทรลเลอร์จะสามารถเขียนสมการได้เป็น
(5)
ทำการเพิ่ม PID Conrtoller ลงไปในแบบจำลองที่เราสร้างขึ้นบนโปรแกรม Simulink จะได้
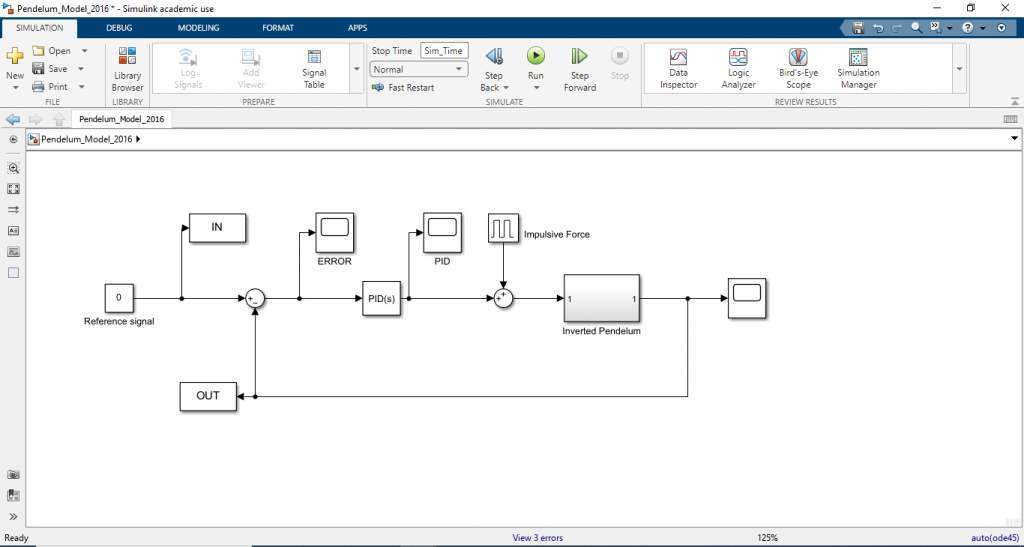
ในงานชิ้นนี้จะใช้การลองผิดลองถูก (trial and error) หาค่าพารามิเตอร์ของ PID Controller ขึ้นมาจำนวนหนึ่ง ซึ่งบางค่าก็ให้ผลตอบสนองที่ดี ทำให้ระบบโดยรวมมีเสถียรภาพ และบางค่าก็ทำให้ผลตอบสนองออกมาไม่ดี ระบบไม่มีเสถียรภาพ ดังตาราง
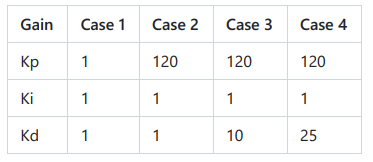
นำค่าพารามิเตอร์ของ PID ข้างต้นไปใส่ลงในสคริปไฟล์ PendulumScript.m ดังนี้
F=1;
M=0.6;
m=0.065;
l=0.178;
I=0.0027;
b=0.1;
g=9.81;
Sim_Time=5;
%PID CONTROLLER
Kp=120;
Ki=1;
Kd=25;
sim('Pendelum_Model_2016');
%Plot
figure
plot(IN.time, IN.data)
hold all
plot (OUT.time, OUT.data)
axis([0, 5, -0.2, 0.2]);
xlabel('Time (Seconds)')
ylabel('Amplitude')
title({'Case 4';' PID Gains: Kp = 120, Ki = 1, Kd = 25'});
lsiminfo(OUT.data, OUT.time)
เมื่อทำการ Run สคริปข้างต้น โปรแกรม Simulink จะทำการ simulation การทำงานโดยจะเห็นว่าระบบควบคุมแบบวงปิดจะพยายามรักษาให้มุมของ Pendulum \(\theta=0\)ผลของจากจำลองระบบจะเป็นดังนี้
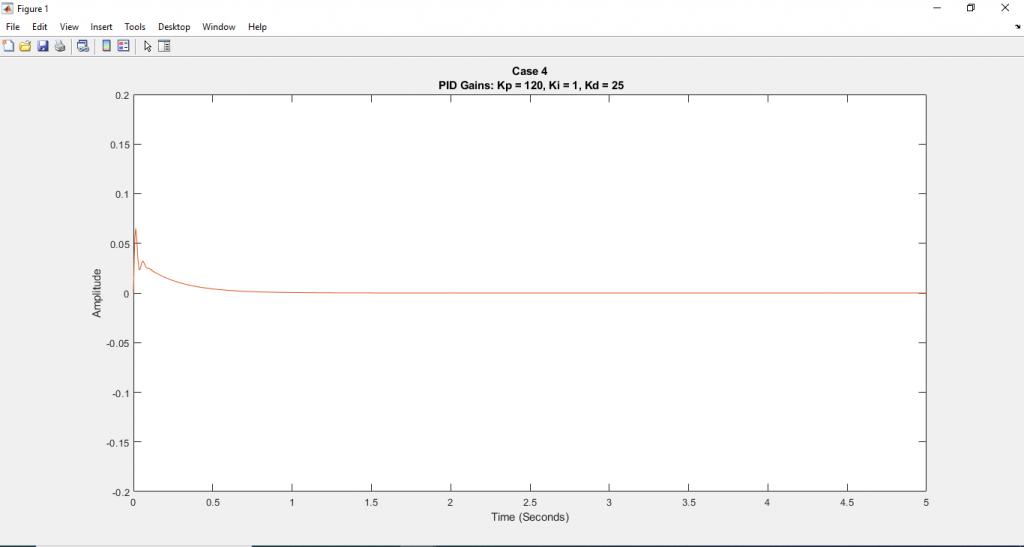
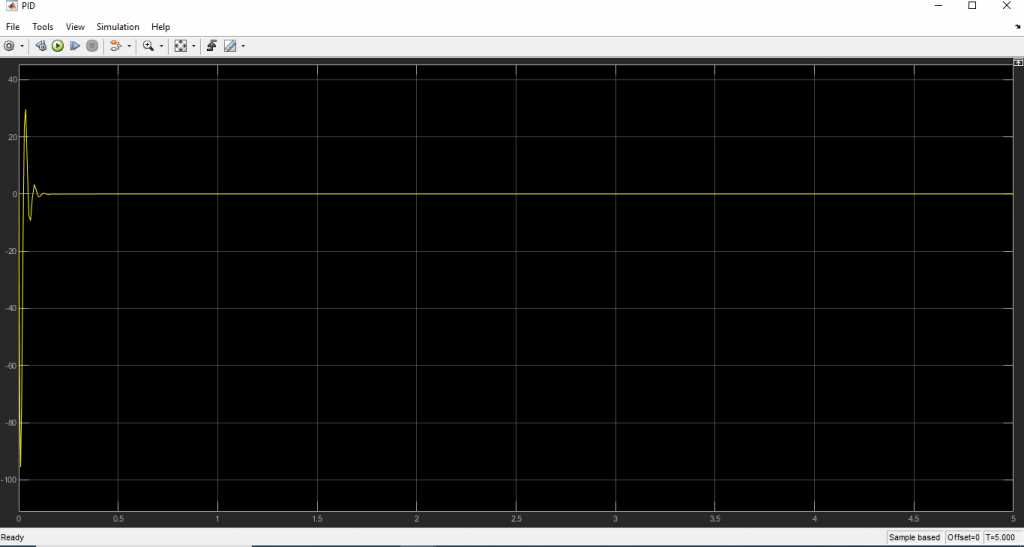
ดาวน์โหลด Simulink file ได้ที่นี่