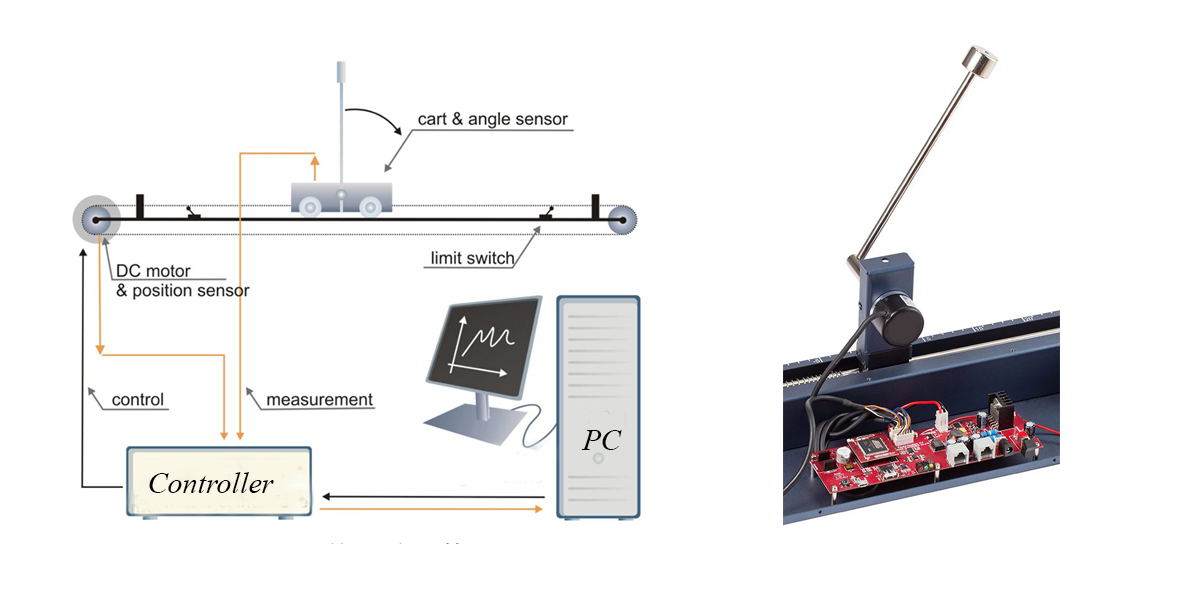
จำลองการควบคุมแบบปิด Inverted Pendulum ด้วยตัวควบคุม LQR โดย Matlab -

จากบล๊อกก่อนหน้านี้ เราได้ศึกษาการหา State Model ของลูกตุ้มกลับหัวกลับไปแล้ว (Inverted Pendulum) https://csys.pro/mimo/2880/ เราจะทดลองเพิ่มตัวควบคุม Linear Quadratic Regulator ซึ่งเป็นคอนโทรลเลอร์ที่มีใช้งานกันอย่างแพร่หลายในระบบการควบคุมที่มีความซับซ้อนแบบ Multiple Inputs/Multiple Outputs (MIMO)

State Space model สามารถเขียนในรูปสมการได้ดังนี้

\(\left\{\begin{matrix} \dot{x}=Ax+Bu \\ y=Cx+Du\end{matrix}\right.\)

(1)

เพื่อให้ระบบเป็นการควบคุมแบบป้อนกลับ จะได้ว่า

\(u=r-Kx\)

(2)

จากสมการ (1) และ (2) สามารถเขียน Block diagram ได้เป็น

แทนสมการ (2) กลับเข้าไปในสมการ (1) จะได้

\(\left\{\begin{matrix} \dot{x}=Ax+B(r-Kx) =(A-BK)x+Br\\ y=Cx+Du\end{matrix}\right.\)

(3)

จากสมการ (3) จะเห็นว่า State Equation มีการเปลี่ยนแปลงไป ค่า K ที่เพิ่มเข้าไปมีผลต่อผลตอบสนองของระบบ ซึ่งการหาค่า K เหมาะสมจะทำให้ระบบมีเสถียรภาพและให้ผลตอบสนองตามที่ผู้ออกแบบต้องการ

การหาค่า K มีหลายวิธี ในบล๊อกนี้จะใช้วิธีการ Linear Quadratic Regulator

เราจะเริ่มที่การวิเคราะห์ว่าระบบที่เราจะควบคุม มีเสถียรภาพหรือไม่ โดยการวิเคราห์ตำแหน่งของโพล จาก Open Loop Transfer function ของ Inverted Pendulum จาก State Space Model ที่ได้ศึกษาไปก่อนหน้านี้ โดยมีตัวอย่างคำสั่ง Matlab ดังนี้

M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;

p = I*(M+m)+M*m*l^2; 

A = [0      1              0           0;
     0 -(I+m*l^2)*b/p  (m^2*g*l^2)/p   0;
     0      0              0           1;
     0 -(m*l*b)/p       m*g*l*(M+m)/p  0];
B = [     0;
     (I+m*l^2)/p;
          0;
        m*l/p];
C = [1 0 0 0;
     0 0 1 0];
D = [0;
     0];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'u'};
outputs = {'x'; 'phi'};

sys_ss = ss(A,B,C,D,'statename',states,'inputname',inputs,'outputname',outputs);

poles = eig(A)

จะ Script ข้างต้น Matlab จะให้ผลลัพธ์ออกมาเป็นตำแหน่งโพลของระบบดังนี้

ซึ่งจะพบว่ามีโพล 2 ตัวที่ทำให้ระบบไม่มีเสถียรภาพ ตัวแรกอยู่ที่ตำแหน่ง 0 ซึ่งอยู่บนแกนจินตภาพของ Complex plan ทำให้ระบบเกิดการ Oscilation หรือหากมี Uncertainites เพียงเล็กน้อยจะทำให้ระบบไม่มีเสถียรภาพทันที และโพลที่ตำแหน่ง 5.5651 เป็นโพลที่อยู่ด้านขวาของ Complex plan ซึ่งมีผลทำให้ระบบไม่มีเสถียรภาพ

ต่อมาเราจะมีวิเคราะห์คุณสมบัติของระบบว่าสามารถควบคุมได้(controllable) หรือไม่ โดยการวิเคราะห์ค่า Rank ของเมตริคความคุมได้ จะต้องเป็น Full Rank ในที่นี้สมการเสตทของ Inverted Pendulum เป็น matrix 4×4 ดังนั้นค่า Rank ของ Controlability Matrix จะต้องเป็นค่า 4

Controlability matrix สามารถเขียนได้ดังนี้

\(\mathbb{C}=\left [ B\, AB\, A^{2}B\cdots A^{n-1}B\right ]\)

(4)

สามารถใช้คำสั่ง Matlab ทำการคำนวณได้ดังนี้

co = ctrb(sys_ss);
controllability = rank(co)

ต่อมาเราจะดำเนินการหาค่า K โดยจะเริ่มที่การพิจารณา Cost function

\(J(u)=\int_{0}^{\infty }(x^{T}Qx+u^{T}Ru)dt\)

(5)

ในทางทฤษฎีสิ่งที่จะต้องทำกับสมการ (5) คือการ minimized ในกรณี Inverted Pendulum เป็นระบบที่มีสมการเสตท 4 ตัว และมี 1 อินพุต ดังนั้น Q จะเป็น Matrx 4×4 และ R จะเป็นค่า Scalar การปรับค่าทั้งสองมีผลต่อค่า K โดยค่า K จะมีขนาดใหญ่ ถ้า Q มีขนาดใหญ่ ในทางตรงข้าม ค่า R ที่มากจะทำให้ค่า K ลดลง

ในการหาค่า K เราจะต้องหา Matrix S ก่อน ซึ่งหาได้จากการแก้สมการ Algrebriac Ricatti Equation (ARE) ดังนี้

\(A^{T}S+SA-SBR^{-1}B^{T}S+Q=0\)

(6)

เมื่อได้ Matrix S สามารคำนวนหาค่า K ได้ดังสมการ

\(K=R^{-1}(B^{T}S)\)

(7)

การคำนวนณทั้งหมดสามารถทำได้โดยใช้ Matlab script ดังนี้

ทดสอบโดยใช้ค่า R=1 ค่า Q คงเดิม

Q = C'*C;
R = 1;
K = lqr(A,B,Q,R)

Ac = [(A-B*K)];
Bc = [B];
Cc = [C];
Dc = [D];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'r'};
outputs = {'x'; 'phi'};

sys_cl = ss(Ac,Bc,Cc,Dc,'statename',states,'inputname',inputs,'outputname',outputs);

t = 0:0.01:5;
r =0.2*ones(size(t));
[y,t,x]=lsim(sys_cl,r,t);
[AX,H1,H2] = plotyy(t,y(:,1),t,y(:,2),'plot');
set(get(AX(1),'Ylabel'),'String','cart position (m)')
set(get(AX(2),'Ylabel'),'String','pendulum angle (radians)')
set(H1, 'Color', 'r');
set(H2, 'Color', 'b');
title('Step Response with LQR Control')

จะได้ผลลัพธ์ K=-1.0 -1.6567 18.6864 3.4594 และผลตอบสนองของระบบเมื่อใช้ K ดังกล่าวในระบบควบคุมแบบปิด เป็นดังนี้

ทดสอบโดยใช้ค่า R=1 ค่า Q เป็นดังนี้

\(Q=\begin{bmatrix} 5000 & 0 & 0 & 0 \\ 0& 0 &0 & 0 \\ 0& 0 &100 &0 \\ 0&0 &0 & 0 \\ \end{bmatrix}\)

โดยมี Matlab script ดังนี้

Q = C'*C;
Q(1,1) = 5000;
Q(3,3) = 100
R = 1;
K = lqr(A,B,Q,R)

Ac = [(A-B*K)];
Bc = [B];
Cc = [C];
Dc = [D];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'r'};
outputs = {'x'; 'phi'};

sys_cl = ss(Ac,Bc,Cc,Dc,'statename',states,'inputname',inputs,'outputname',outputs);

t = 0:0.01:5;
r =0.2*ones(size(t));
[y,t,x]=lsim(sys_cl,r,t);
[AX,H1,H2] = plotyy(t,y(:,1),t,y(:,2),'plot');
set(get(AX(1),'Ylabel'),'String','cart position (m)')
set(get(AX(2),'Ylabel'),'String','pendulum angle (radians)')
title('Step Response with LQR Control')

จะได้ผลลัพธ์ K=-70.7107 -37.8345 105.5298 20.9238 และผลตอบสนองของระบบเมื่อใช้ K ดังกล่าวในระบบควบคุมแบบปิด เป็นดังนี้