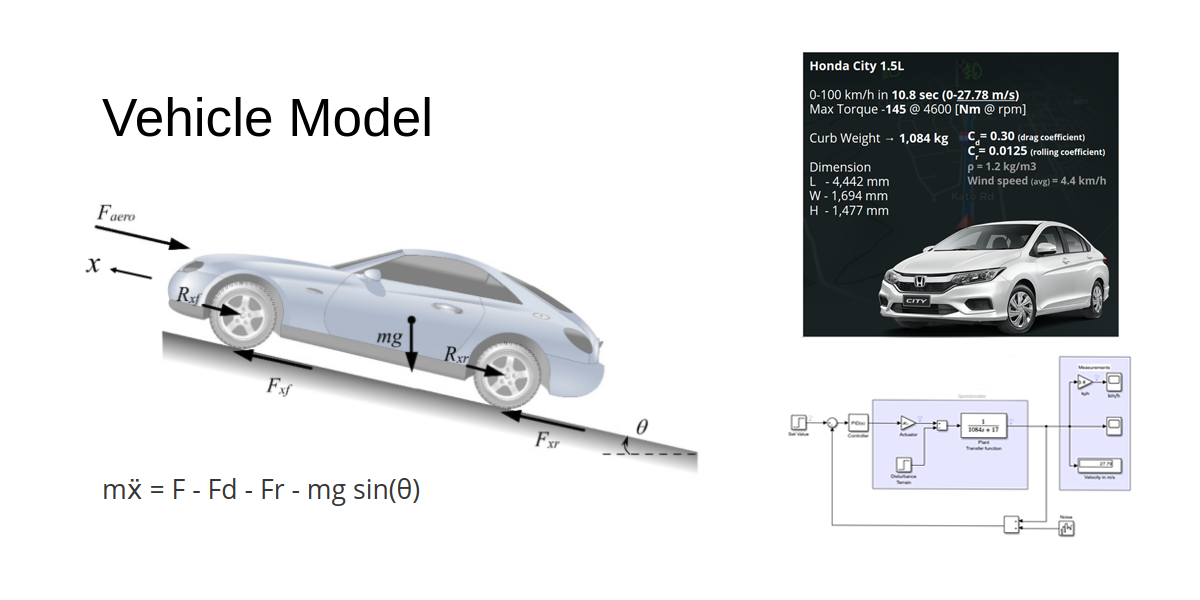
Simple free body diagram ของรถยนต์แสดงได้ดังภาพ
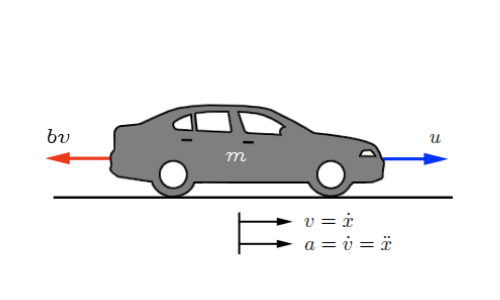
จากกฎข้อที่สองของนิวตัน เขียนสมการพลศาสตร์ได้เป็น
(1)
จัดรูปสมการ (1) ใหม่จะได้
(3)
m คือมวลของรถ
x คือระยะทางการเคลื่อนที่
b คือสัมประสิทธิแรงเสียดทาน
v คือความเร็วรถ
u คือแรงขับเคลื่อนรถจากเครื่องยนต์
จากคู่มือ Honda City 1.5L เราจะพบค่าพาริเตอร์ที่จำเป็นต่อการออกแบบระบบดังภาพ

เริ่มจากการกำหนดว่าเราต้องการรักษาระดับความเร็วรถไว้ที่ 100 Km/hour
(4)
คำนวณหา Drag force อันเกิดจากลมที่เข้ามาปะทะตัวรถ
(5)
คำนวณหา Rolling resistance force อันเกิดจากพื้นถนน
(6)
คำนวณสัมประสิทธิแรงเสียดทาน
(7)
คำนวณหา Norminal force ที่ผลิตได้จากเครื่องยนต์
(8)
เมื่อได้ค่าพารามิเตอร์ ครบถ้วนแล้ว จากนั้นให้ทำการ Take Laplace สมการ (3)
(9)
จัดรูปสมการ (9) จะได้ Transfer function ของระบบดังนี้
(10)
นำสมการ ค่าที่ได้จา (5) (6) (8) และ สมการ (10) ไปวาดบล๊อกไดอะแกรมใน Matlab/Simulink จะได้ดังภาพ
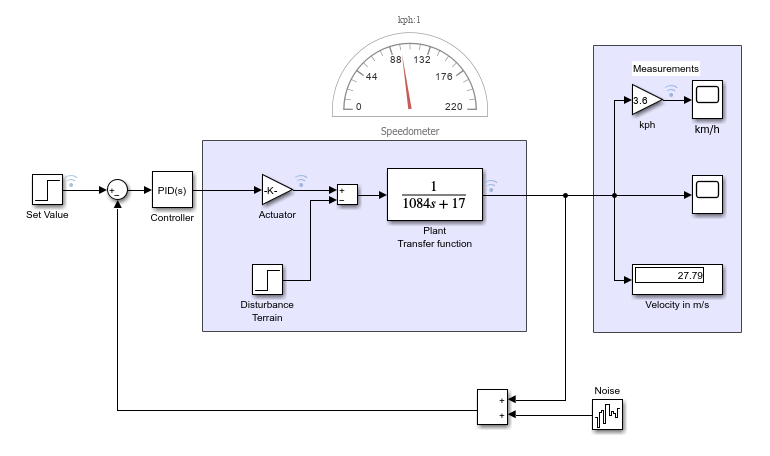
โดยเราจะใช้แบบจำลองข้างภาพ ออกแบบตัวควบคุมพีไอดี ให้ผลตอบสนองของระบบเป็นดังนี้
Rise Time < 12 Sec. ( การเพิ่มความเร็วจาก 0 – 100 km/h)
Overshoot < 10% (ความเร็วอันเกิดจากการเร่งกำลังไปถึง 100km/h จะมีค่า < +/- 10%)
Steady state error < 2% (การรักษาระดับความเร็วที่ 100km/H อนุญาตให้มี error < +/- 2%)

นอกจากนี้ยังสามารถวิเคราะห์เสถียรภาพของระบบได้ด้วย matlab script ดังนี้
m = 1084; %mass
b = 17; %damping coefficient
u = 475.72; %nominal force
r = 27.78; %desired speed
Gs = tf(1, [m, b]); % s-domain
Ts = 1; % sampling time
Gz = c2d(Gs, Ts); % z-domain
% analysis of step response
figure(1)
step(u*Gs)
% Open-loop poles/zeros
figure(2)
pzmap(Gz)
axis([-1 1 -1 1])
% Open-loop Bode plot
figure(3)
bode(Gz)
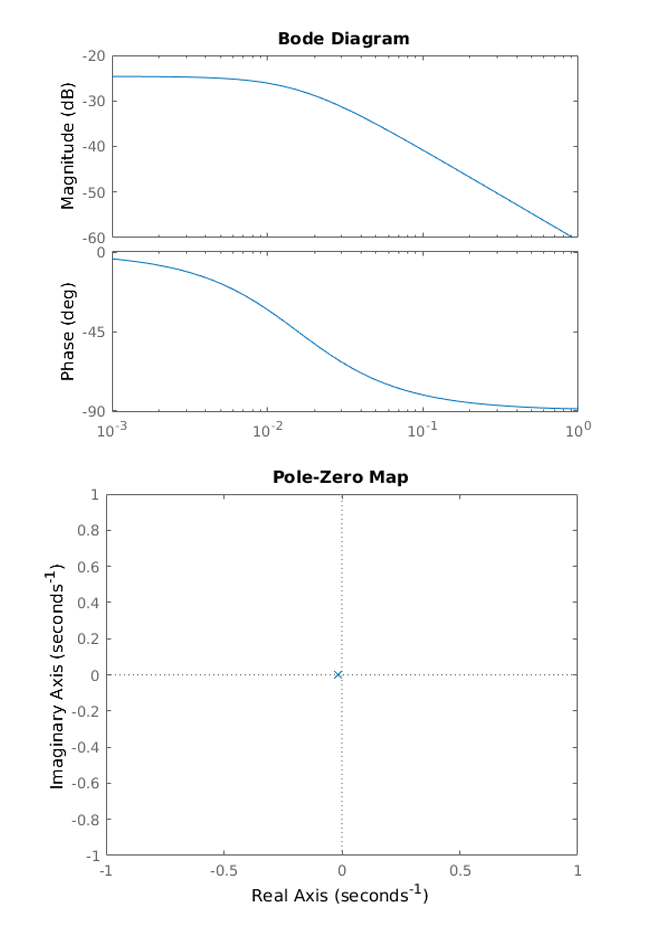
ดาวน์โหลดไฟล์ Matlab/Simulink ได้ที่นี่