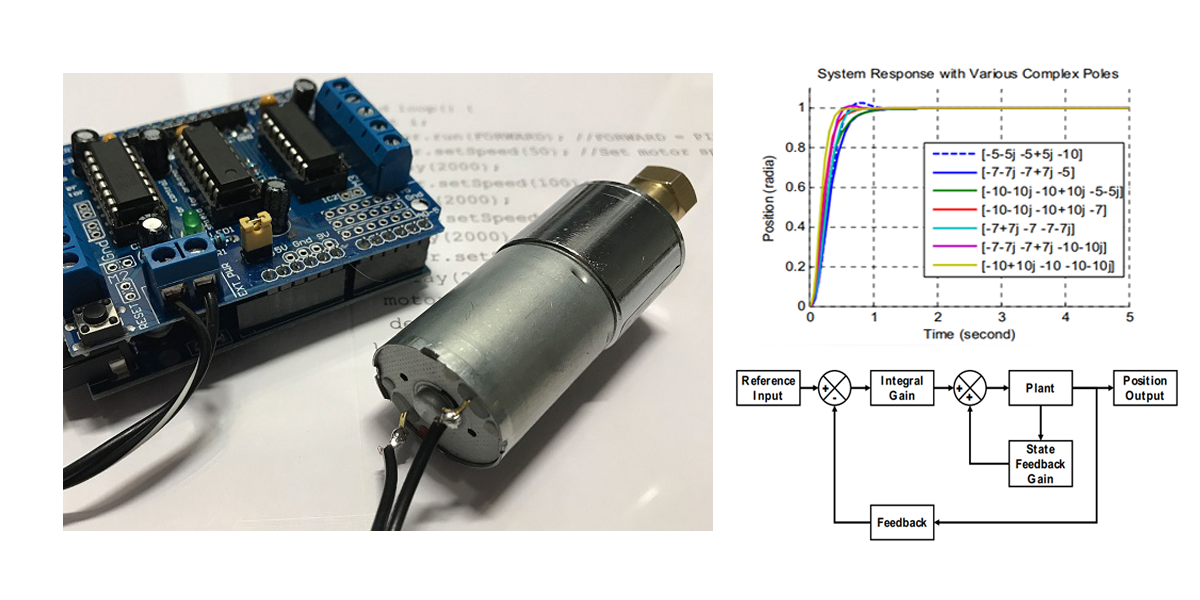
การควบคุมตำแหน่งการหมุนของ DC Motor เป็นแอพพลิเคชั่นที่เรียกว่า เซอร์โวมอเตอร์ที่เราเห็นกันในอุตสาหกรรม เพราะโดยปกติแล้ววัตถุประสงค์หลักของการเลือกใช้เซอร์โว ก็เพื่อต้องการนำมาใช้ในการควบคุมตำแหน่งการหมุนเป็นหลัก
การควบคุมตำแหน่งจะมีความซับซ้อนมากกว่าการควบคุมความเร็วเพราะมี Feedback Loop เพิ่มเข้ามาอีก 1 ลูป ซึ่งในบล๊อกนี้เราจะนำเสนอตัวควบคุมแบบ Integral เพิ่มเข้ามาในลูบนอกสุด แสดงได้ดังรูป
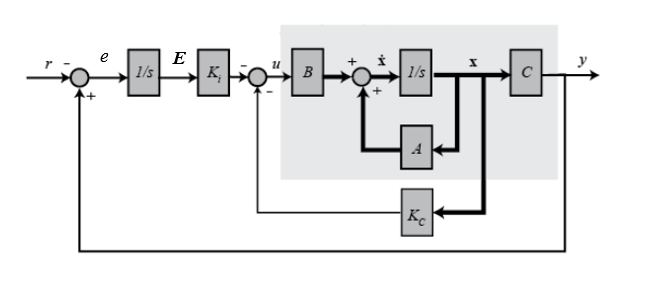
การออกแบบ Position Control จะประกอบด้วย 2 ขั้นตอน 1) ใช้วิธีการ Pole placement ที่ได้ศึกษาไปแล้วในบล็อกก่อนหน้า เลือกผลตอบสนองของ DC Motor ตามใจต้องการ ด้วยวิธี Pole Placement การหาค่า K เพื่อให้ระบบตำแหน่งของ Pole ตามที่เราต้องการ 2) ทำการเพิ่ม Position control close Loop
มาเริ่มขั้นตอนที่ 1
จากบล๊อก จำลองการทำงาน DC Motor ในรูปแบบสมการเสตท (State Equation) โดย Matlab เราจะได้สมการเสตทของ DC Motor ดังนี้
(1)
จัดรูปสมการใหม่
(2)
จากบล๊อก เลือกผลตอบสนองของ DC Motor ตามใจต้องการ ด้วยวิธี Pole Placement ทำให้เราทราบวิธี pole placement สำหรับหาค่า Kc เพื่อให้ระบบมีโพลตามที่เราต้องการ
สมมติว่าเราต้องการวางโพล 3 ตำแหน่งลงในระบบ ประกอบด้วย p1=-10+10i , p2=-10-10i , p3=-20;
โดยมอเตอร์ดีซี มาพารามิเตอร์ดังต่อไปนี้
J=0.01; %moment of inertia
b=0.1; %friction coefficient
K=0.075; %motor constant
R=1; %armature resistance
L=0.5; %inductance
เราสามารถคำนวณหาค่า Kc โดยใช้สคริปดังนี้
J=0.01; %moment of inertia
b=0.1; %friction coefficient
K=0.075; %motor constant
R=1; %armature resistance
L=0.5; %inductance
%state with pole placement
A=[0 1 0
0 -b/J K/J
0 -K/L -R/L]
B=[0 ; 0 ; 1/L]
C=[1 0 0]
D=[0];
%desire poles
p1=-10+10i;
p2=-10-10i;
p3=-20;
%pole placement calculation gains K
Kc=place(A,B,[p1,p2,p3]);
%step unit test
t=0:0.001:20;
step(A-B*Kc,B,C,D,1,t)
จะได้ผลตอบสนองดังนี้
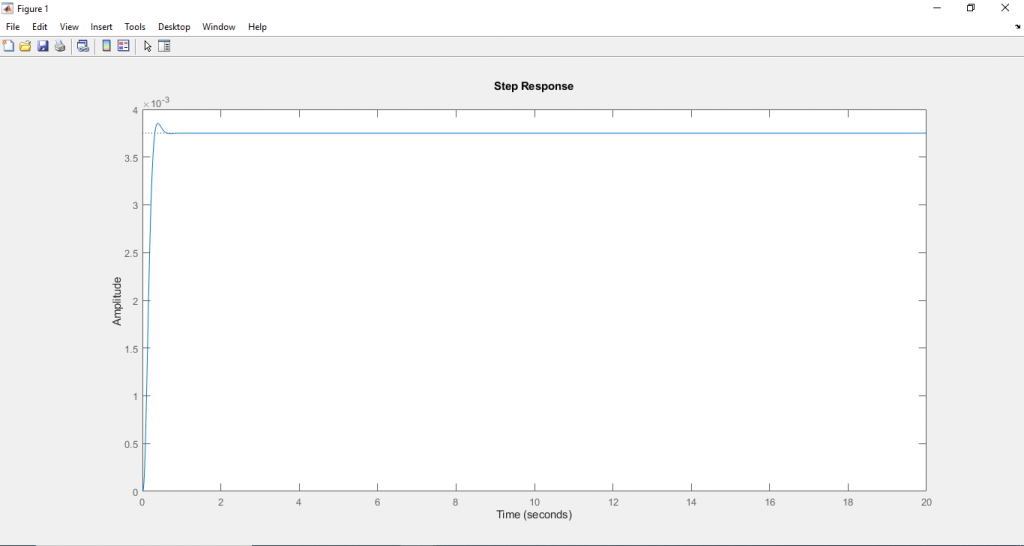
จะรูปผลตอบสนองเราพบว่าระบบมี Overshoot และ Settling ตามที่เราต้องการ แต่ผลตอบสนองอาจจะยังไม่ลู่เข้าสู่ค่าที่เรากำหนด การเพิ่มตัวควบคุม Intergral เข้าจะไปจะแก้ปัญหาดังกล่าวได้
สมการเสตทสามารถเขียนได้ว่า
(3)
จากรูปที่ 1 เขียนอินพุตของระบบได้ใหม่เป็น
(4)
พิจารณาเทอม \(k_{i}e\) จะได้ว่า
(5)
เปลี่ยนสมการ (5) เป็นตัวควบคุมแบบอินทิเกรท
(6)
แทนสมการ (4) ลงใน (3) จะได้
(7)
สมการ (5) จะกลายเป็น Matrix 4×4 โดยให้ \(k_{i}=1\) ประกอบด้วยสมการดังนี้
(8)
ทำการทอสอบ Position Control หลังจากเพิ่ม Integral Loop ได้โดยสคริปดังนี้
J=0.01; %moment of inertia
b=0.1; %friction coefficient
K=0.075; %motor constant
R=1; %armature resistance
L=0.5; %inductance
%state with pole placement and integral
Aa=[0 1 0 0
0 0 1 0
0 0 -b/J K/J
0 0 -K/L -R/L];
Ba=[ -1 ; 0 ; 0 ; 0];
Bau=[0 ; 0 ; 0 ; 1/L ];
Ca=[0 1 0 0];
Da=[0];
%desire poles
p1=-10+10i;
p2=-10-10i;
p3=-20;
p4=-30;
Kc=place(Aa,Bau,[p1,p2,p3,p4]);
%step unit test
t=0:0.001:20;
step(Aa-Bau*Kc,Ba,Ca,Da,1,t)
ได้ผลตอบสนองที่ลู่เข้าหา Set point ดังนี้
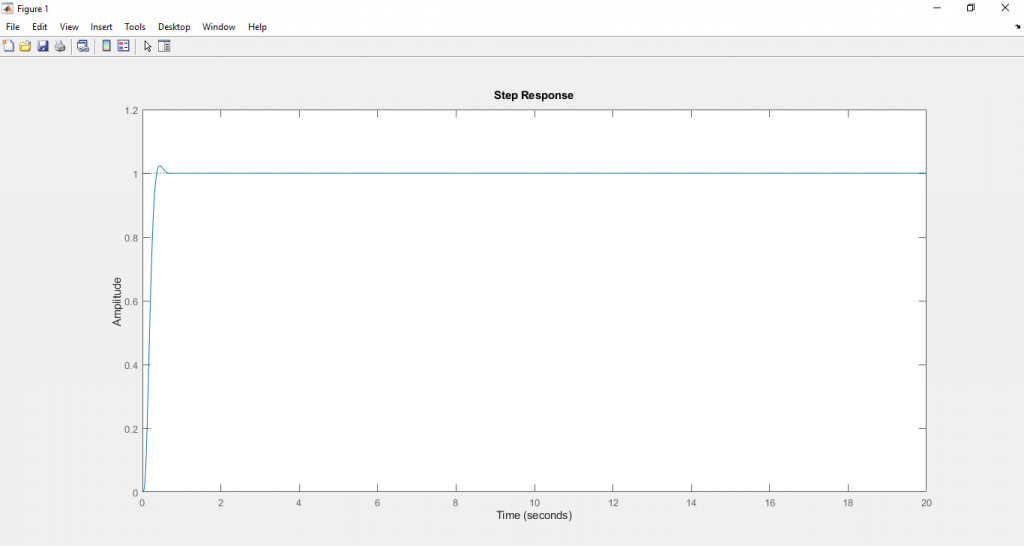
นอกจากการรันสคริปแล้ว เรายังสามารถทดสอบระบบโดยการใช้โปรแกรม Simulink โดยเราจะใช้สมการ (2) ในการวางคอนโทรลบล๊อกไดอะแกรม แสดงได้ดังภาพ
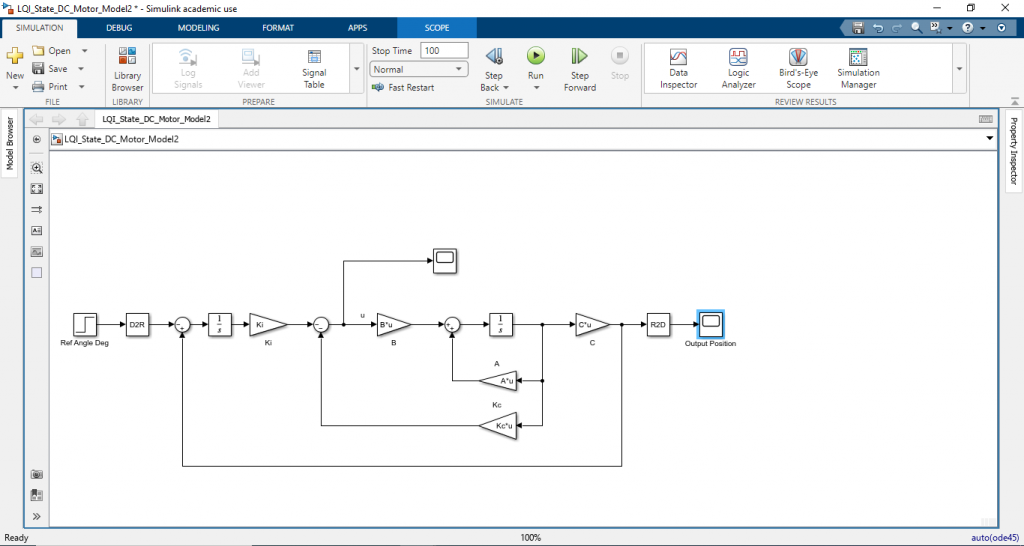
และทำการรับสคริปดังนี้
%motor parameter
%sim with I_State_DC_Motor_Model2.slx
A=[0 1 0;0 -10 7.5;0 -0.15 -2];
B=[0; 0; 2];
C=[1 0 0];
% Integral Constant
Ki=300;
% Desire poles
p1=-10+10i;
p2=-10-10i;
p3=-20;
%pole placement calculation gains K
Kc=place(A,B,[p1,p2,p3]);
open('I_State_DC_Motor_Model2.slx')
sim('I_State_DC_Motor_Model2.slx')
จะได้ผลลัพธ์ดังนี้
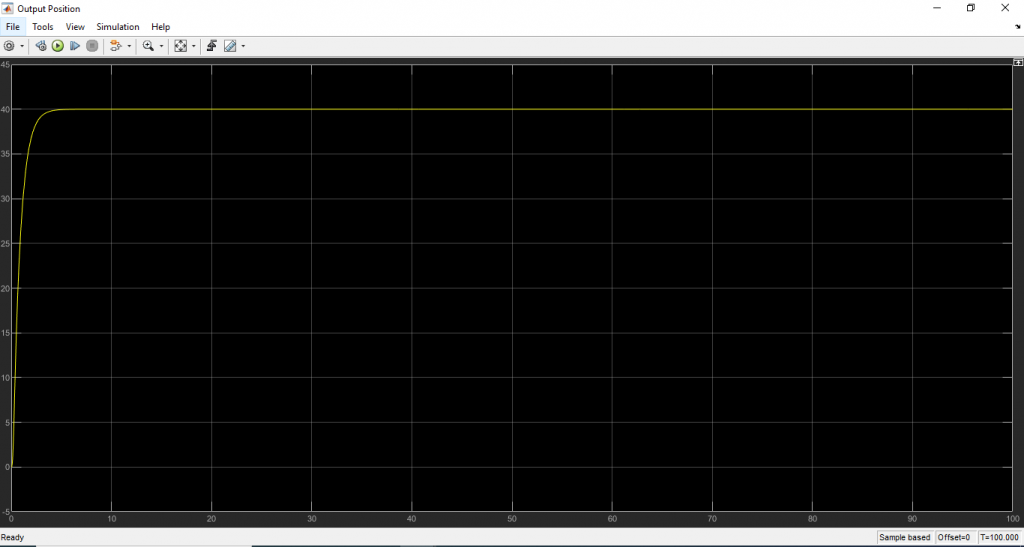
ดาวน์โหลดไฟล์สคริปได้ที่นี้