จะขอใช้ตัวอย่างจากบล๊อก ตัวสังเกตุแบบเต็มเสตท(Full State observer) โดย Matlab/Simulink และ การหาสมการเสตทของลูกตุ้มกลับหัว (Inverted Pendulum) ด้วยวิธีพลังงาน และจำลองระบบโดย Matlab มาเป็นตัวอย่างในการศึกษา โดยในบล๊อกนี้เราจะลองการทำงานของ Inverted Pendulum ด้วยวิธีการ Transfer function และจำลองการทำงานตัวสังเกตุ ด้วยวิธีการสมการเสตท(State space equation) และเพิ่ม Integral Action เพื่อตัวควบคุมระบบ
การออกแบบตัวสังเกตุแบบเต็มเสตท แต่ตัวควบคุมแบบอินทริเกรท มีขั้นตอนดังนี้
1) คำนวณหาค่า K ซึ่งจะใช้วิธีการ pole placement ศึกษาได้จากบล๊อก เลือกผลตอบสนองของ DC Motor ตามใจต้องการ ด้วยวิธี Pole Placement
2) คำนวณค่า Nbar เพื่อปรับสัญญาณอ้างอิง r ให้มีขนาดเสกลเดียวกับ y=Cx เช่นถ้าลู่เข้าหา 0.6 ( y=0.6) และ r เป็น unit step แสดงได้ดังรูป
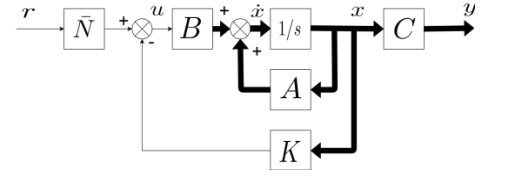
การคำนวณหา \(\bar{N}\) เขียนเป็นสมการอย่างง่ายได้ว่า
(1)
3)คำนวณหาค่า L โดยคำนวณตาม Ogata
จากรูปที่ 1 จะเห็นว่า system state matrix คือ (A-BK) และ observer state matrix คือ (A-LC) โครงสร้างของทั้งสองเมทริคมีความเหมือนกัน จะแตกต่างกันที่ลำดับการวางตำแหน่งของเมทริคไม่ทราบค่า BK และ LC
จากทฤษฎีเราทราบว่า Eigen value ของ (A-LC) และ (A-LC)T เหมือนกัน จึงสามารถเขียน observer state matrix ให้มีลำดับการวางของตำแหน่งเช่นเดียวกัน system state matrix ดังนี้
(2)
สมการ Full state observer แสดงได้ดังนี้
(3)
เราจึงสามารถใช้วิธีการ Pole placement กับสมการ (3) เช่นเดียวกับ system state matrix (A-BK)
(4)
โดยที่ \( \mu \) คือตำแหน่งโพลที่ต้องการ ปกติแล้วมักจะออกแบบให้ State Observer มีการตอบสนองเร็วกว่าระบบที่ถูกควบคุม
จากจะสมการ (4) เราพบว่า
(5)
ทั้งนี้หากระบบเป็นระบบที่สังเกตุได้(Observable) ค่า L จะคำนวณได้เสมอ
คำนวณ Matrix \(A_{o}\) ของ Observer ได้ดังนี้
(6)
4) นอกจากนี้แล้วเพื่อควบคุมระบบให้เข้าสู่ค่า Set points จะมีการเพิ่มตัวควบคุมแบบ Integral เข้าไปด้วย ผู้สนใจสามารถศึกษาได้จากบล๊อก จำลอง การควบคุมตำแหน่ง(Position) ของดีซีมอเตอร์ ด้วยวิธี State Integral Control โดย Matlab/Simulink
นำสมการ (1) – (6) มาทำการจำลองการทำงานโดย Matlab Simulink โดยวางคอนโทรลบล๊อกไดอะแกรมดังภาพ
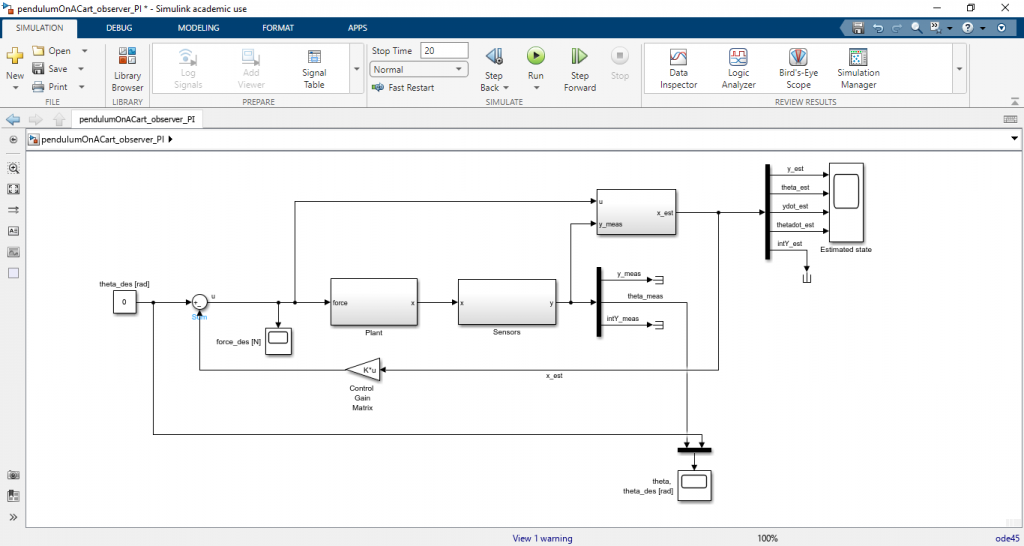
ทำการรันสคริป
clear;
clc;
close all;
% plant params (physical values)
g = 9.81; % gravity [m/s^2]
cM = 5; % Cart mass [kg]
pL = 0.25; % pendulum length [m]
pm = 1; % pendulum mass [kg]
% model parameter non-perfect characterization
cM_model = cM+0.2;
pL_model = pL-0.1;
pm_model = pm-0.15;
A = [0 0 1 0 0
0 0 0 1 0
0 (-pm_model*g)/cM_model 0 0 0
0 ((cM_model+pm_model)*g)/(cM_model*pL_model) 0 0 0
1 0 0 0 0];
B = [0
0
1/cM_model
-1/(cM_model*pL_model)
0];
C = [1 0 0 0 0
0 1 0 0 0
0 0 0 0 1];
D = 0;
sys = ss(A,B,C,D);
fprintf('\nControllability:\n\trank(ctrb(sys))=%d\n',rank(ctrb(sys)));
%% Initial values
theta_init = 0.2; % initial pendulum angle [rad]
dTheta_init = 2.0; % initial pendulum angular velocity [rad/s]
%% Controller
% use pole placement to determine K
p1 = -2 + 1i;
p2 = -2 - 1i;
p3 = -1.0000 + 0.2506i;
p4 = -1.0000 - 0.2506i;
p5 = -3;
K = place(A,B,[p1 p2 p3 p4 p5]);
figure;
pzmap(ss(A-B*K,B,C,D)); title('controller');
xlim([-12 1]);
%% Observer
fprintf('\nObservability:\n\trank(obsv(sys))=%d\n',rank(obsv(sys)));
% use pole placement to determine L
p1 = -10 + 10i;
p2 = -10 - 10i;
p3 = -5.0000 + 0.2506i;
p4 = -5.0000 - 0.2506i;
p5 = -8;
L=(place(A',C',[p1 p2 p3 p4 p5]))';
figure;
pzmap(ss(A-L*C,B,C,D)); title('observer');
xlim([-12 1]);
จะได้ผลลัพธ์ดังนี้
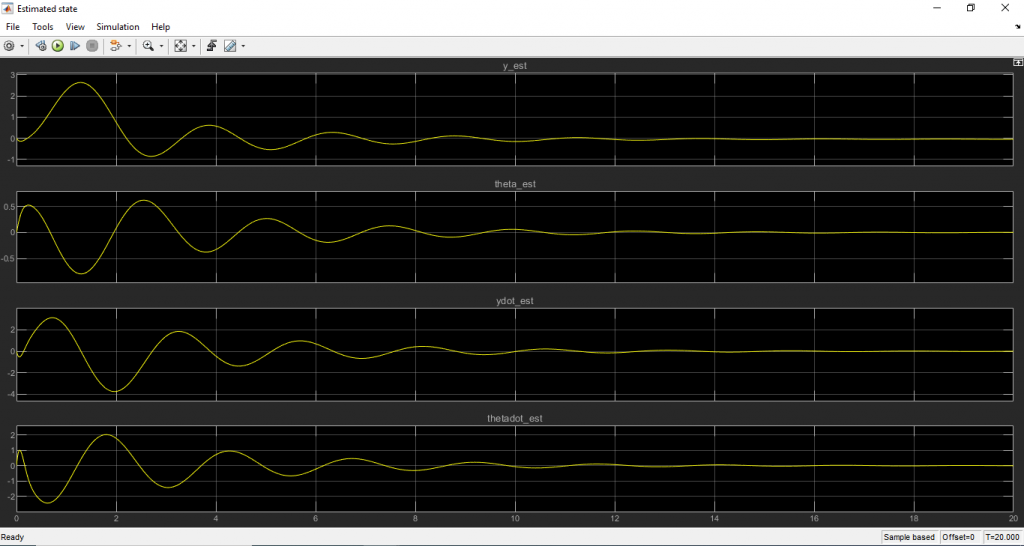

โหลดไฟล์ Matlab/Simulink ได้ที่นี่