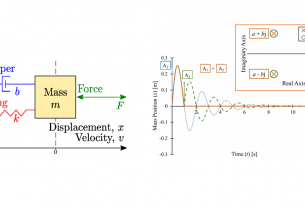
จากที่ก่อนหน้านี้เราได้ทำความรู้จักกับวงจร RLC แบบอนุกรม และได้ทำการจองการทำงานโดยใช้โปรแกรม Matlab/Simulink ไปแล้วในหัวข้อ จำลองการทำงานของ วงจร RLC อนุกรม โดย Matlab/Simulink https://csys.pro/sim/2833/
ในบล๊อกนี้เราจะศึกษาการจำลองการทำงานของระบบพลศาสตร์โดยสมการสเตท(State variable) ซึ่งจะเป็นพื้นฐานนำไปสู่การควบคุมแบบ Mutiple Inpts/Multiple Outputs(MIMO) ที่มีความซับซ้อนสูงขึ้น สมการสเตทสามารถเขียน block diagram ได้เป็น
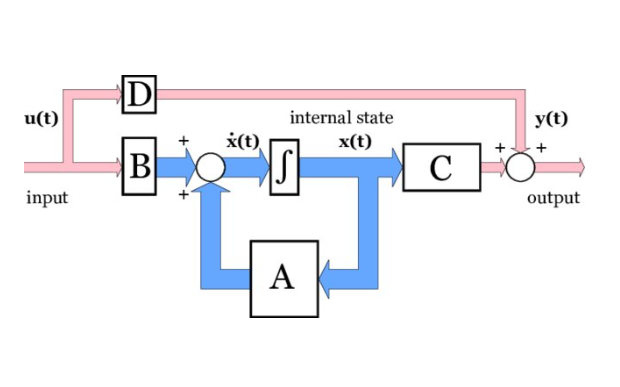
จากบล๊อกไดอะแกรม สามารถเขียนเป็นสมการได้เป็น
(1)
จาก blog ก่อนหน้านี้เราพบว่า วงจร RCL สามารถเขียนสมการพลศาสตร์ได้ดังนี้
(2)
จัดรูปสมการ (2) ใหม่อีกครั้งเพื่อเปลี่ยนจากสมการอนุพันธ์อันดับสอง เป็นสมการสเตท โดยกำหนดให้
(3)
ทำการ derivative สมการ (3) จะได้
(4)
เขียนสมการ (4) ใหม่ ตามรูปแบบของสมการ (1)
(4)
จากสมการ (4) เราจะพบว่า
เราต้องการให้ผลตอบสนองของระบบเป็น \( y(t)=u_{c}\) ดังนั้นจะสามารถเขียนสมการเอาพุตของสเตทได้เป็น
(5)
จากสมการ (5) เราจะพบว่า
เมื่อได้ Matrix A , B , C และ D ครบถ้วนแล้วเราจะนำ Matrix เหล่านี้ไปสร้างเป็นสมการสเตทบนโปรแกรม Matlab เพื่อจำลองการทำงานของวงจร RLC แบบอนุกรม โดยกำหนดพารามิเตอร์ของวงจร RLC ดังนี้
C=0.1 uF
R=100 Ohm
L=0.004 mH;
Vi = square wave ความถี่ 500hz และมี duty cycle 50%
Matrix A, B, C และ D ที่ได้จากด้านบน
นำค่าพารามิเตอร์ทั้งหมดมาสร้างเป็น matlab script ทำหน้าที่เป็นฟังชั่น ให้สามารถถูกเรียกใช้ แล้วบันทึกเป็นไฟล์ชื่อ RLC.m ดังนี้
function dx=RLC(t,x)
%-----------------Define parameters--------------------%
C=0.1e-6;
R=100;
L=4e-3;
freq = 500; % Frecuency (Hz)
d_cycle = 50; % Duty cycle (%)
V_in = 2.5*(1+square(2*pi*freq*t,d_cycle));
%-------------define state variable---------------%
dx=zeros(2,1); %create array
dx(1)=x(2);
dx(2)=(1/(L*C))*(-R*C*x(2)-x(1)+V_in);
ให้ทำการสร้าง matlab script ขึ้นมาอีกหนึ่งไฟล์ ตั้งชื่อว่า State_var_RLC.m ซึ่งจะหน้าที่สองอย่าง อย่างแรกคือคือเป็นโปรแกรมหลักในการเรียกใช้ function RLC ที่อยู่ในไฟล์ RLC.m และอย่างที่สองคือทำหน้าที่ในการพล๊อตกราฟผลตอบสนองของระบบ ดังนี้
%call function RLC
[t,x]=ode45(@RLC, [0 0.01], [0 0]);
%Plot result
figure(1)
plot(t,x(:,1));
grid on;
title("Capacitor Volatge");
xlabel("Time");
ylabel("Voltage");
ทำการ RUN สคริปไฟล์ State_var_RLC.m จะได้ผลลัพธ์ดังนี้
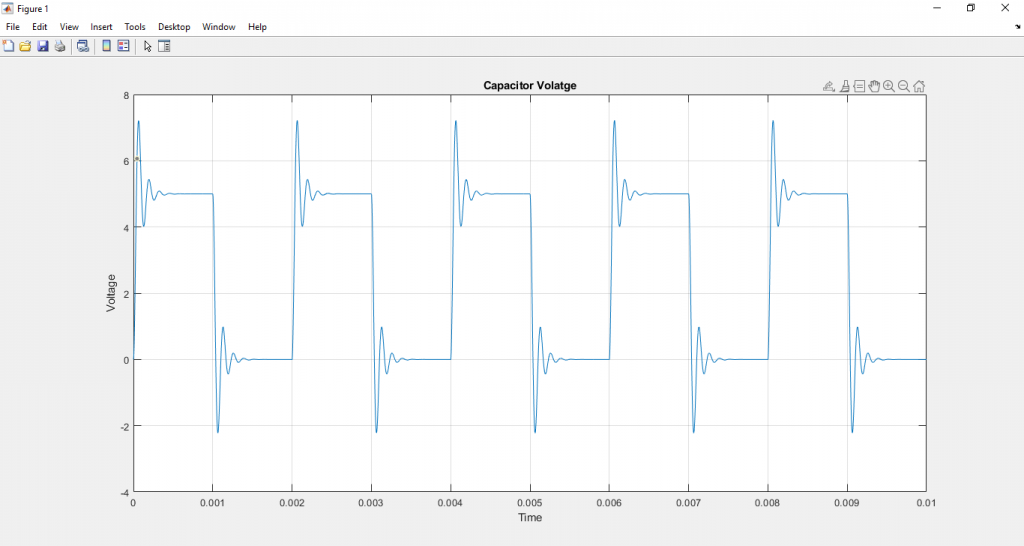
ดาวน์โหลด matlab file ได้ที่นี่