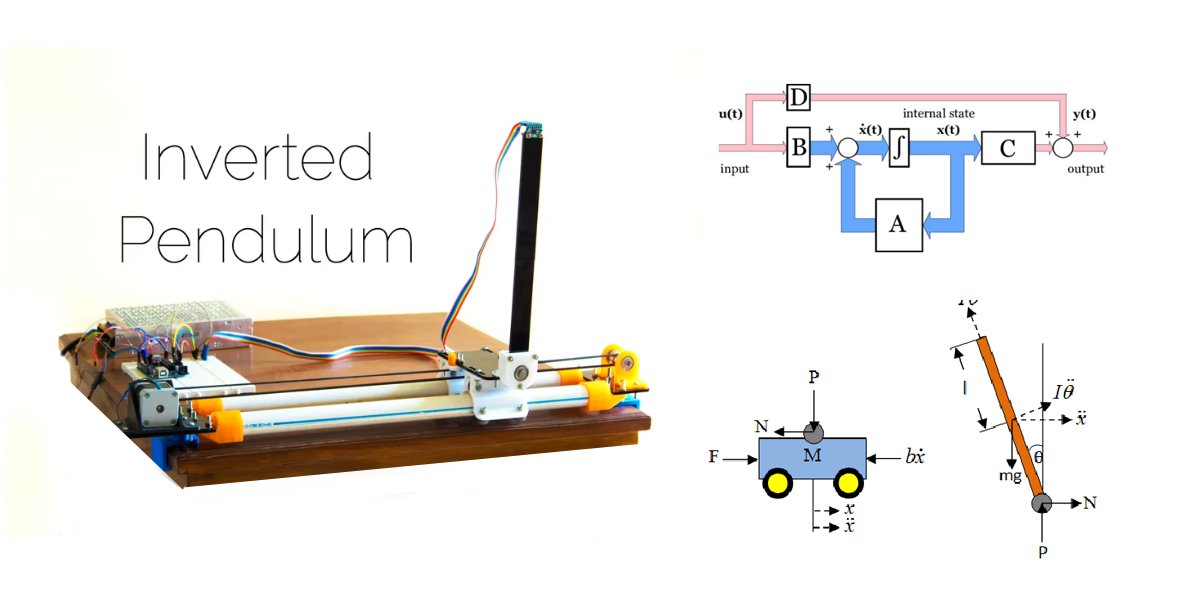
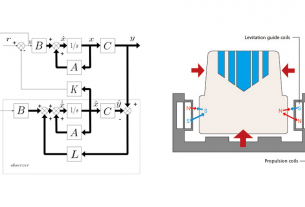
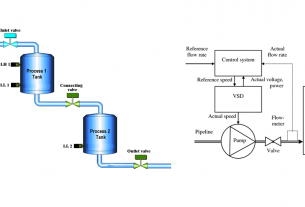
State space model ของลูกตุ้มกลับหัว (Inverted Pendulum) โดยกฎข้อที่สองของนิวตัน และจำลองการทำงานโดย Matlab -

Free body diagram ของลูกตุ้มกลับหัวสามารถเขียนได้หลายแบบ ผู้เขียนขอยกแบบที่นิยมที่สุด โดยสามารถแยกออกได้ 2 ส่วน คือ ส่วนของรถ และส่วนของ Pendulum ดังแสดงได้ดังภาพด่านล่าง

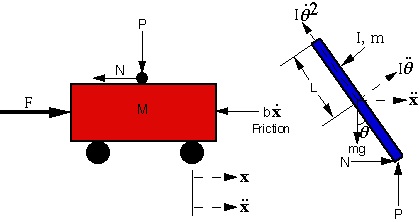
x ตำแหน่งของรถ
m มวลของ Pendulum
M มวลของรถ
b สัมประสิทธิ์แรงเสียดทานของรถ
I โมเม้นความเฉื่อยของ Pendulum
l ระยะจากจุดหมุนถึงศูนย์กลางมวลของ Pendulum
F แรงที่กระทำต่อรถ
\(\theta\) มุมของ Pendulum

\(M\ddot{x}+b\dot{x}+N= F\)

(1)

และ Pendulum ในแนวการเคลื่อนที่ติดไปกับตัวรถใน ในแกน x จะได้

\(N=m\ddot{x}=ml\ddot{\theta} cos\theta -ml\dot{\theta} ^{2}sin\theta\)

(2)

แทนค่าสมการ (2) ลงใน สมการ (1) จะได้

\((M+m)\ddot{x}+b\dot{x}+ml\ddot{\theta }cos\theta -ml\dot{\theta }^{2}sin\theta =F\)

(3)

พิจารณาผลรวมของแรงที่ตั้งฉากกับ Pendulum จะได้

\(-Psin\theta +Ncos\theta -mgsin\theta =ml\ddot{\theta}+m\ddot{x}cos\theta \)

(4)

พิจารณาผลรวมโมเม้นที่กระทำกับ Pendulum รอบจุดศูนย์กลางมวล จะได้

\(-Plsin\theta -Nlcos\theta =I\ddot{\theta }\)

(5)

แทนสมการ (5) ลงใน (4) จะได้

\((I+ml^{2})\ddot{\theta }+mglsin\theta =-ml\ddot{x}cos\theta \)

(6)

สมการ (3) และ (6) เป็นสมการพลศาสตร์ไม่เชิงเส้นของระบบอินเวิร์สเพนดูลัม ที่เราจะนำไปใช้งานต่อไป

จากรูปที่ 1 สมการพลศาสตร์ (3) และ (6) พบว่ามุม \(\theta \) ให้คำตอบที่เป็นจริงทั้งตำแหน่ง pendulum ทิ้งตัวคว่ำลงในแนงดิ่ง และหงายขึ้นตั้งฉากกับรถ จึงสามารถกำหนด มุม \(\theta \) ได้ตามรูปที่ 3

รูปที่ 3. กำหนดการอ้างอิงมุมแกว่ง \(\phi \)

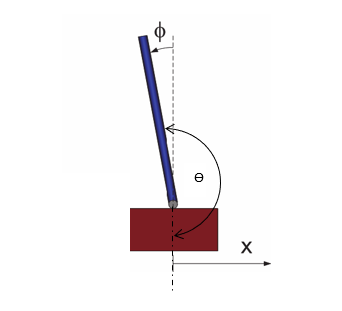
กำหนดให้ \(\theta =\pi +\phi\) โดยที่ \(\phi\) คือมุมแกว่งแคบๆ ของปลาย Pendulum เราจะได้ \(cos(\pi +\phi )\approx -1\) และ \(sin(\pi +\phi )\approx -\phi\) ดังสามารถทำ Linearization ให้สมการ (3) และ (7) เป็นเชิงเส้นรอบๆ จุด \(\theta=\pi\)

\((M+m)\ddot{x}+b\dot{x}+ml\phi =u\)

(7)

\((I+ml^{2})\ddot{\phi }-mgl\phi =ml\ddot{x}\)

(8)

ทำการ Take Laplace สมการ (7) และ (8)

\((M+m)X(s)s^{2}+bX(s)s+ml\Phi(s)s^{2} =U(s)\)

(9)

\((I+ml^{2})\Phi(s)s^{2}-mgl\Phi(s) =mlX(s)s^{2}\)

(10)

จัดรูปสมการ (12) จะได้

\(X(s)=\left [ \frac{I+ml^{2}}{ml}-\frac{g}{s^{2}} \right ]\Phi (s)\)

(11)

แทนค่าสมการ (11) กลับลงใน (9) จะได้

\((M+m)\left [ \frac{I+ml^{2}}{ml}-\frac{g}{s^{2}} \right ]\Phi (s)s^{2}+b\left [ \frac{I+ml^{2}}{ml}-\frac{g}{s^{2}}\right ]\Phi (s)-ml\phi (s)s^{2}=U(s)\)

(12)

จัดรูปสมการ (14) จะได้ Transfer function ของ Pendulum

\(T_{pen}=\frac{\Phi (s)}{U(s)}=\frac{\frac{ml}{q}s}{s^{3}+\frac{b(I+ml^{2})}{q}s^{2}-\frac{(M+m)mgl}{q}s-\frac{bmgl}{q}}\)

(13)

โดยที่ \( q=(M+m)(I+ml^{2})-ml^{2}\)

แทนสมการ (13) กลับเข้าไปใน สมการ (10) จะได้ Transfer function ของรถ

\(T_{car}=\frac{X(s)}{U(s)}=\frac{\frac{(I+ml^{2})s^{2}-gml}{q}}{s^{4}+\frac{b(I+ml^{2})}{q}s^{3}-\frac{(M+m)mgl}{q}s^{2}-\frac{bmgl}{q}s}\)

(14)

ต่อไปเราจะหา สมการ State โดยกำหนดให้

\(\begin{pmatrix} \dot{x}_{1} \\ \dot{x}_{2}\\ \dot{x} _{3}\\ \dot{x}_{4}\end{pmatrix}=\begin{pmatrix} \dot{x} \\ \ddot{x}\\ \dot{\phi }\\ \ddot{\phi }\end{pmatrix}\)

สามารถเขียนสมการ (7) และ (8) ใหม่ได้เป็น

\((M+m)\dot{x}_{2}+bx_{2}-ml\dot{x}_{4} =u\)

(15)

\((I+ml^{2})\dot{x}_{4}+mglx_{3} =ml\dot{x}_{2}\)

(16)

แทน (16) ลงใน (15)

\(\dot{x}_{2}=\ddot{x}=-\frac{b(I+ml^{2})}{q}x_{2}+\frac{m^{2}gl^{2}}{q}x_{3}+\frac{(I+ml^{2})}{q}u=-\frac{b(I+ml^{2})}{q}\dot{x}+\frac{m^{2}gl^{2}}{q}\Phi+\frac{(I+ml^{2})}{q}u\)

(18)

แทน (18) ลงใน (16)

\(\dot{x}_{4}=\ddot{\Phi }=-\frac{bml}{q}x_{2}+\frac{(M+m)mgl}{q}x_{3}+\frac{ml}{q}u=-\frac{bml}{q}\dot{x}+\frac{(M+m)mgl}{q}\Phi+\frac{ml}{q}u\)

(19)

จาก สมการ (18) และ (19) จะได้ว่า

\(A=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0&-\frac{b(I+ml^{2})}{I(M+m)-Mml^{2}} & \frac{m^{2}gl^{2}}{I(M+m)-Mml^{2}} & 1 \\ 0& 0 & 0 & 0 \\ 0 &-\frac{bml}{I(M+m)-Mml^{2}} & \frac{(M+m)mgl}{I(M+m)-Mml^{2}} & 0\\ \end{bmatrix}\)

\(B=\begin{bmatrix} 0 \\ \frac{(I+ml^{2})}{I(M+m)-Mml^{2}}\\ 0\\ \frac{ml}{I(M+m)-Mml^{2}} \\\end{bmatrix}\)

\(C=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix}\)

ทดลองใช้ Matlab หา Transfer function ดังนี้

M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;
q = (M+m)*(I+m*l^2)-(m*l)^2;
s = tf('s');

P_cart = (((I+m*l^2)/q)*s^2 - (m*g*l/q))/(s^4 + (b*(I + m*l^2))*s^3/q - ((M + m)*m*g*l)*s^2/q - b*m*g*l*s/q);

P_pend = (m*l*s/q)/(s^3 + (b*(I + m*l^2))*s^2/q - ((M + m)*m*g*l)*s/q - b*m*g*l/q);

sys_tf = [P_cart ; P_pend];

inputs = {'u'};
outputs = {'x'; 'phi'};

set(sys_tf,'InputName',inputs)
set(sys_tf,'OutputName',outputs)

sys_tf

ทดลองใช้ Matlab หา State model ดังนี้

M = .5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;

p = I*(M+m)+M*m*l^2; %denominator for the A and B matrices

A = [0      1              0           0;
     0 -(I+m*l^2)*b/p  (m^2*g*l^2)/p   0;
     0      0              0           1;
     0 -(m*l*b)/p       m*g*l*(M+m)/p  0];
B = [     0;
     (I+m*l^2)/p;
          0;
        m*l/p];
C = [1 0 0 0;
     0 0 1 0];
D = [0;
     0];

states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'u'};
outputs = {'x'; 'phi'};

sys_ss = ss(A,B,C,D,'statename',states,'inputname',inputs,'outputname',outputs)