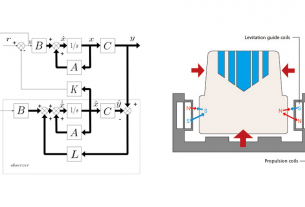
จากที่เราเคยได้ศึกษาการหาแบบจำลองแบบ Single Input/Sigle Output (SISO) ของ DC มาแล้วในบล๊อก จำลองการทำงาน DC Motor ด้วย Matlab/Simulink ครั้งนี้เราจะมีจัดรูปสมการของ DC Motor ให้เป็นแบบ State Model
จากวงจรไฟฟ้าของดีซีมอเตอร์ ดังรูปที่ 1
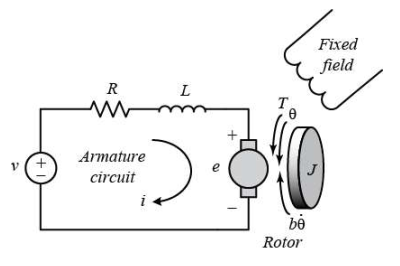
J คือโมเม้นความเฉื่อยของโรเตอร์ (0.01 kg.m^s)
b คือสัมประสิทธิความหนืดของโรเตอร์ (0.1 N.m.s)
Ke คือค่าคงที่แรงเคลื่อนไฟฟ้า (0.01 V/rad/s)
Kt คือค่าคงที่แรงบิดของมอเตอร์ (0.01 N.m/A)
R คือค่าความต้านทานขดลวดอาเมเจอร์ (1 Ohm)
L คือค่าการนำไฟฟ้าของขดลวดอาเมเจอร์ (5 H)
สมการแรงบิดของมอเตอร์สามารถเขียนได้ดังนี้
(1)
แรงดัน Back E.M.F. มีสมการคือ
(2)
ปกติ ดีซีมอเตอร์ จะออกแบบให้ \(K_{e}=K_{t}\) เราจึงมักใช้สัญลักษณ์ \(K\)
จากกฎข้อที่สองของนิวตัน เราจะได้สมการไดนามิคทางกลดังนี้
(3)
และจาก Kirrchoff Voltage Law จะได้สมการทางไฟฟ้าดังนี้
(4)
Take Laplace transform สมการ (3) และ (4) จะได้
(5)
(6)
แทนสมการ (6) ลงใน สมการ (5) จะได้ Transfer function ดังนี้
(7)
ทำการจัดรูปสมการ (3) และ (4)
(8)
(9)
เขียนสมการ (8) และ (9) ในรูป Matrix จะได้ดังนี้
(10)
และกำหนดให้ความเร็ว เป็นผลตอบของระบบ จะได้สมการ
(11)
ทดสอบการทำงานโดยการรับ Script ดังนี้
% Motor parameter
J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;
% State Model
A = [-b/J K/J
-K/L -R/L];
B = [0
1/L];
C = [1 0];
D = 0;
sys = ss(A,B,C,D);
% Open Loop Step Test
step(sys)
จะได้ผลลัพธ์ดังนี้
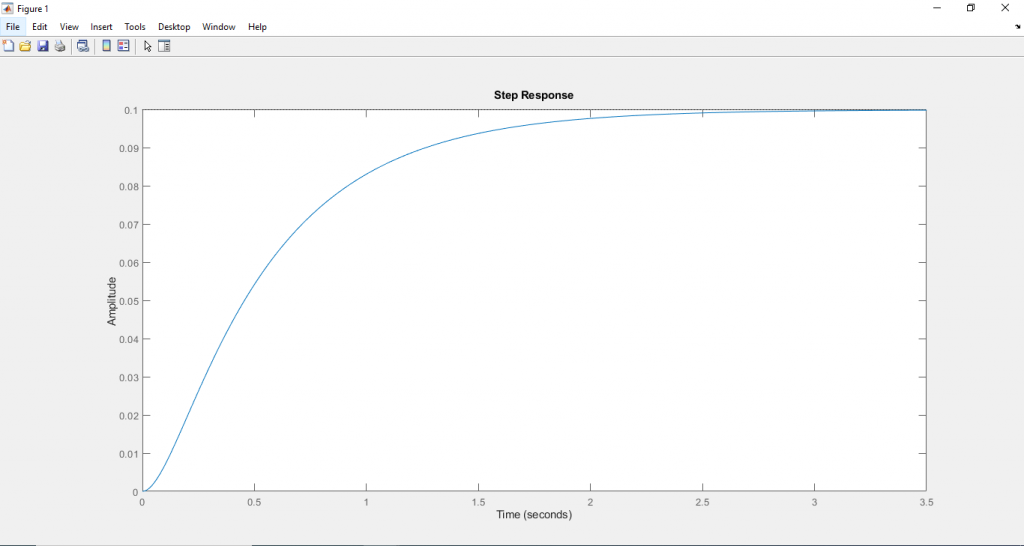
ดาวน์โหลด Matlab script ได้ที่นี่