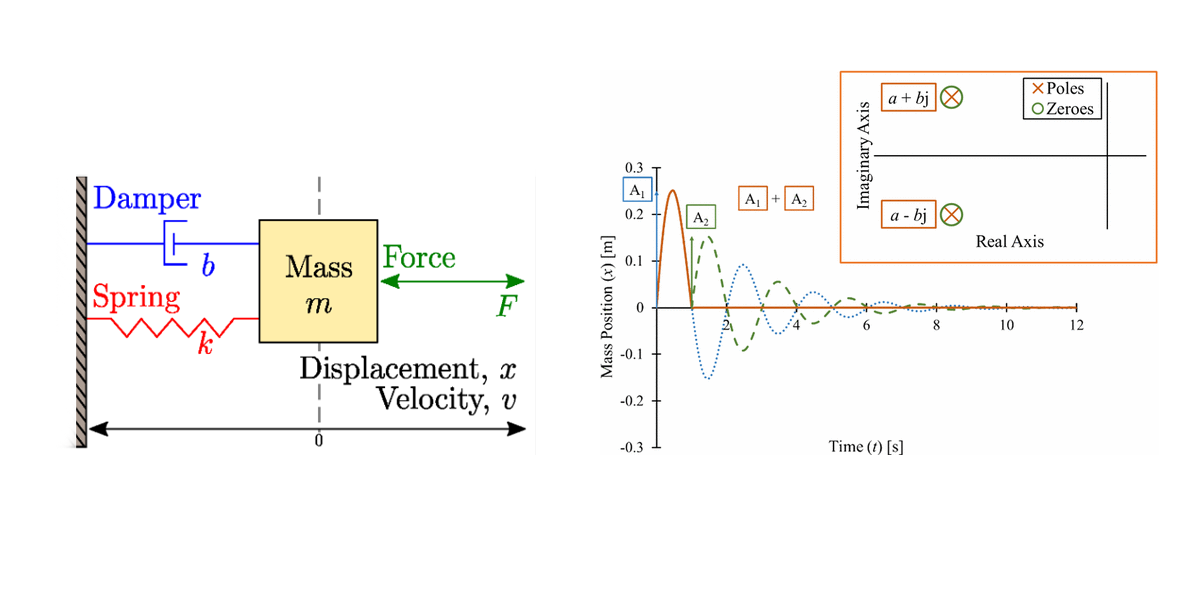
Mass spring damped system นอกจากจะเขียนสมการพลศาสตร์ในรูป SISO แล้ว ยังสามารถเขียนอยู่ในรูปของ State Equation ได้ด้วย โดยสามารถเขียน Free body diagram ได้ดังนี้
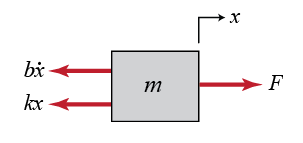
จากกฎข้อที่สองของนิวตัน เราสามารถเขียนสมการพลศาสตร์ ได้ดังนี้
\(m\ddot{x}+b\dot{x}+kx=F\)
(1)
m คือน้ำหนักของมวล
b คือสัมประสิทธิแรงเสียดทาน
k คือสัปประสิทธิของสปริง
F คือแรงที่กระทำต่อมวล
จัดรูปสมการ (1)
\(\ddot{x}=-\frac{b}{m}\dot{x}-\frac{k}{m}x+\frac{F}{m}\)
(2)
สมการเสตท สามารถเขียนในเป็นบล๊อกไดอะแกรมได้ดังนี้
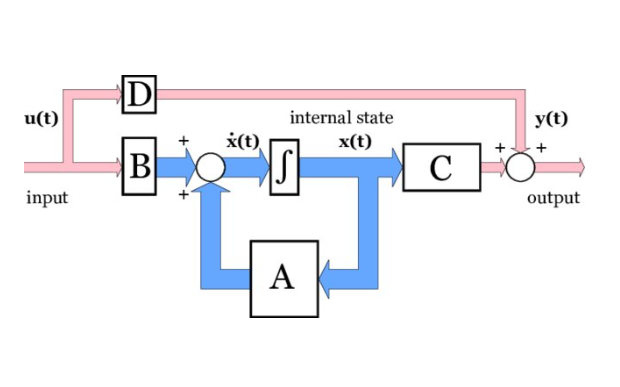
เราสามารถเปลี่ยนสมการ (1) ให้อยู่ในรูปของ สมการเสตท โดยการกำหนดตัวแปรเสตทดังนี้
\(X=\begin{bmatrix}
x \\
\dot{x}\end{bmatrix}\)
(3)
ทำดิฟเฟอเรนชิเอต สมการ (3) หนึ่งครั้งจะได้
\(\dot{X}=\begin{bmatrix}
\dot{x} \\
\ddot{x}\end{bmatrix}\)
(4)
แทนสมการ (2) ลงใน สมการ (4)
\(\dot{X}=\begin{bmatrix}
\dot{x} \\
\ddot{x}\end{bmatrix}=\begin{bmatrix}
0 & 1 \\
-\frac{k}{m} & -\frac{b}{m} \\
\end{bmatrix}+\begin{bmatrix}
0 \\
\frac{1}{m}\end{bmatrix}F\)
(5)
และสมการเอาพุตของสมการเสตท เขียนได้ดังนี้
\(y=\begin{bmatrix}
1 & 0 \\
\end{bmatrix}\begin{bmatrix}
x \\
\dot{x}\end{bmatrix}\)
(6)
ทดสอบการจำลองได้โดย Script ดังนี้
%mass spring damp parameter
m = 1;
k = 1;
b = 0.2;
F = 1;
% Put into Matrix
A = [0 1; -k/m -b/m];
B = [0 1/m]';
C = [1 0];
D = [0];
% Make it be state equation
sys = ss(A,B,C,D);
% Step test
step(sys)
legend('MSD to Step')
จะได้ผลลัพธ์ดังนี้
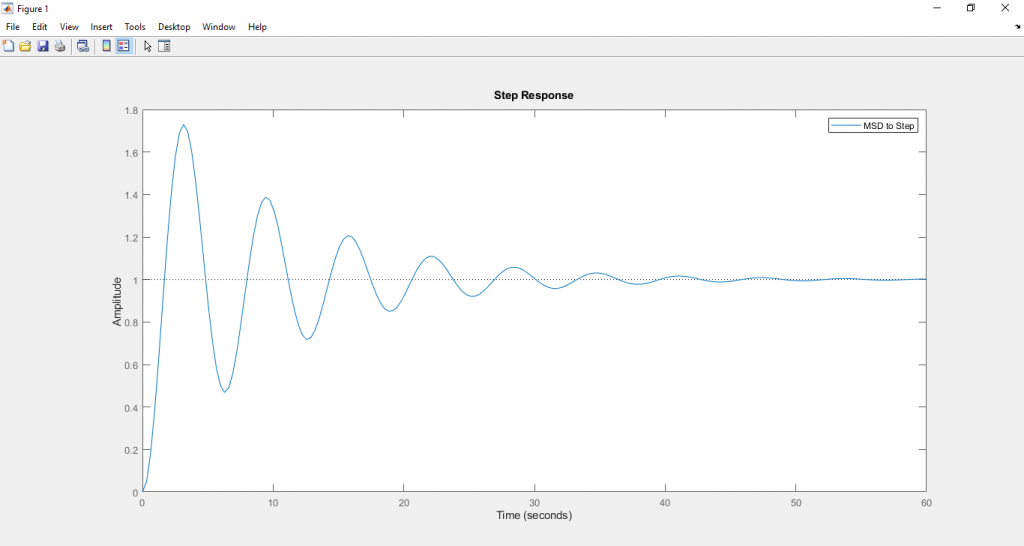
ดาวน์โหลดไฟล์ Matlab ได้ที่นี้