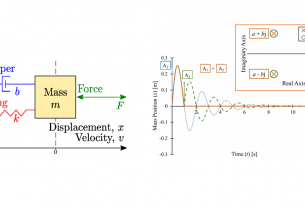
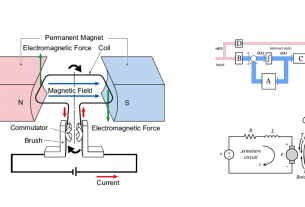
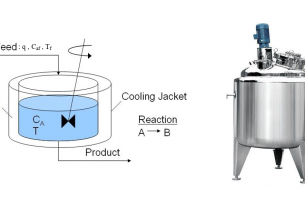
แบบจำลองเสตท การลอยตัวด้วยแรงแม่เหล็ก (State model of magnet levitation) -

Simple free body diagram ของระบบลอยตัวด้วยแม่เหล็กแสดงได้โดยภาพดังนี้

สามารถเขียนสมการได้ดังนี้

ความเร็วของมวลแสดงได้โดย

\(\frac{dx}{dt}=v\)

(1)

จากกฎข้อที่สองของนิวตันจะได้

\(M\ddot{x}=Mg-c\left ( \frac{i}{0.1-x} \right )^{2}-f_{v}v\)

(2)

M คือมวล (0.491 kg)
g ความเร่งจากแรงโน้มถ่วง (9.81 m/s^2)
\(f_{v}\)คือสัมประสิทธิแรงเสียดทานของอากาศ 0.04 Ns/m
c คือค่าคงที่แรงแม่เหล็ก (0.3 Nm/A^2)
L คือค่าอินดักแต๊น (0.2H)
R คือค่าความต้านทาน (50 Ohm)
x คือค่าระยะการยก (กำหนดไว้ 0.06m)

จัดรูปสมการ (2)

\(\frac{dv}{dt}=-g+\frac{c}{M}\left ( \frac{i}{0.1-x} \right )^{2}-\frac{f_{v}}{M}v\)

(3)

จาก Kirchhoff voltage law จะได้สมการ

\(V=V_{R}+V_{L}=iR+L\frac{di}{dt}\)

(4)

จัดรูปสมการ (4)

\(\frac{di}{dt}=-\frac{R}{L}i+\frac{V}{L}\)

(5)

กำหนดให้

\(\begin{bmatrix} x \\ \dot{x}\\ i\end{bmatrix}=\begin{bmatrix} x_{1} \\ x_{2}\\ x_{3}\end{bmatrix}\)

สมการ (1) , (3) และ (5) สามารถจัดรูปใหม่ได้เป็น

\(\left\{\begin{matrix} \dot{x_{1}} =x_{2}\\ \dot{x}_{2}=-g+\frac{c}{M}\frac{x_{3}^{2}}{0.1-x}-\frac{f_{v}x_{2}}{M}\\ \dot{x_{3}}=\frac{1}{L}(-Rx_{3}+V)\end{matrix}\right.\)

(6)

จะได้สมการไม่เชิงเส้น เราจะควบคุมระบบรอบๆ จุดสมดุลหนึ่งเท่านั้น จึงต้องทำการ Linearized สมการ (6) โดยการคำนวณหาจุดสมดุล

ให้สมการ (6) = 0 จะได้

\(\left\{\begin{matrix} x_{2}=0\\ -g+\frac{c}{M}\frac{x_{3}^{2}}{0.1-x}-\frac{f_{v}x_{2}}{M}=0\\ \frac{1}{L}(-Rx_{3}+V)=0\end{matrix}\right.\)

(7)

แทนค่าลงในสมการ (7)

\(\left\{\begin{matrix} x_{2}=0\\ -9.81+\frac{0.3}{0.491}\frac{x_{3}^{2}}{0.1-0.06}-\frac{0.04x_{2}}{0.491}=0\\ \frac{1}{0.2}(-50x_{3}+V)=0\end{matrix}\right.\)

(8)

จะได้จุดสมดุล 2 จุดคือ \(x_{1}=0.06\; x_{2}=0\; x_{3}=-0.800983\) และ \(x_{1}=0.06\; x_{2}=0\; x_{3}=0.800983\) โดย \(x_{3}\) มีสองค่าทั้งนี้ก็เพราะกระแสวิ่งทางใดก็ได้เกิดอำนาจแม่เหล็กทั้งสองทาง ซึ่งในบล็อกนี้จะขอใช้ค่าบวก

ทำการ Linearization รอบจุดสมดุล

\(A=\begin{bmatrix} \frac{\partial f}{\partial x_{1}} &\frac{\partial f}{\partial x_{2}} &\frac{\partial f}{\partial x_{3}} \\ \frac{\partial g}{\partial x_{1}} &\frac{\partial g}{\partial x_{2}} &\frac{\partial g}{\partial x_{3}} \\ \frac{\partial h}{\partial x_{1}} &\frac{\partial h}{\partial x_{2}} &\frac{\partial h}{\partial x_{3}} \\ \end{bmatrix}\)

(9)

แทนสมการ (6) และค่าที่ได้จากการแก้สมการ (8) ลงในสมการ (9)

\(A=\begin{bmatrix} 0 & 1 & 0 \\ \frac{0.611x_{3}^{2}}{(0.1-x_{1})^{2}}&-0.0814 &\frac{1.222x_{3}}{-0.1-x_{1}} \\ 0& 0 & -250 \\ \end{bmatrix}\)

\(A=\begin{bmatrix} 0 & 1 & 0 \\ 245 &-0.0814 & -24.47 \\ 0& 0 & -250 \\ \end{bmatrix}\)

(10)

สามารถเขียนเป็นสมการเสตทได้ดังนี้

\(\dot{x}=\begin{bmatrix} 0 & 1 & 0 \\ 245 &-0.0814 & -24.47 \\ 0& 0 & -250 \\ \end{bmatrix}x+\begin{bmatrix} 0 \\ 0\\ \frac{1}{L}\end{bmatrix}V\)

(11)

ทำการทดสอบระบบโดยการรับสคริปบน Matlab ดังนี้

%state parameters
A = [ 0   1   0
     245 -0.0814 -24.47
      0   0  -250];

B = [ 0
      0
      5 ];

C = [ 1 0 0 ];

%pole location

poles = eig(A)

t = 0:0.01:2;
u = zeros(size(t));
x0 = [0.01 0 0];

sys = ss(A,B,C,0);

[y,t,x] = lsim(sys,u,t,x0);
plot(t,y)
title('Open-Loop Response to Non-Zero Initial Condition')
xlabel('Time (sec)')
ylabel('Ball Position (m)')

จะได้ผลตอบสนองดังนี้

จากสคริป พบว่าระบบมีโพล ดังนี้ poles = 15.6118 ,-15.6932 , -250.0000 จะพบว่ามีโพล 1 ตัวอยู่ด้านขวาของ Complex plan ซึ่งทำให้ระบบไม่มีเสถียรภาพ สอดคล้องกับกราฟผลตอบสนองระยะของ x เพิ่มมากขึ้นเรื่อยๆ หมายถึงอำนาจแม่เหล็กไม่สามารถยึดเหนี่ยวมวลไว้ในตำแหน่งทำงาน หลุดร่วงออกห่างจากจุดทำงานมากขึ้นเรื่อยๆ

ดาวน์โหลด matlab file ได้ที่นี่