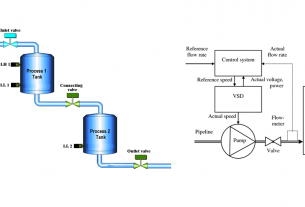
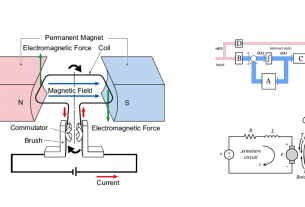
ตัวสังเกตุแบบเต็มเสตท(Full State observer) โดย Matlab/Simulink -

ระบบที่เราจะควบคุมจะมีตัวแปรเสตท \(x\) ที่ต้องนำมาใช้เป็นสัญญาณป้อนกลับ แต่บ่อยครั้งไม่สามารถวัดค่าได้ด้วยเครื่องมือวัดจึงจำเป็นที่จะต้องใช้การคำนวณเสตท \(\hat{x}\) จากแบบจำลองทางพลศาสตร์ แนวคิด State observer แสดงได้ดังภาพ

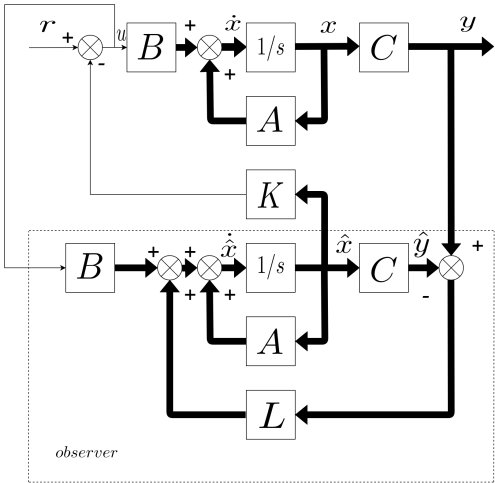
State observer ก็คือการสร้างแบบจำลองคู่ขนานกับระบบพลศาสตร์จริง เพื่อประมาณค่าตัวแปรเสตทของระบบจริงนั้นเอง ตัวสังเกตุ(Observer) มีวิธีการออกแบบหลายวิธี บล๊อกนี้จะขอใช้วิธีตามหนังสือ Modern Control Engineering เขียนโดย Prof. Mitsuhiko Ogata

จะขอใช้ตัวอย่างจากบล๊อก แบบจำลองเสตท การลอยตัวด้วยแรงแม่เหล็ก (State model of magnet levitation) มาเป็นตัวอย่างในการศึกษา

การออกแบบตัวสังเกตุแบบเต็มเสตท มีขั้นตอนดังนี้

1) คำนวณหาค่า K ซึ่งจะใช้วิธีการ pole placement ศึกษาได้จากบล๊อก เลือกผลตอบสนองของ DC Motor ตามใจต้องการ ด้วยวิธี Pole Placement

2) คำนวณค่า Nbar เพื่อปรับสัญญาณอ้างอิง r ให้มีขนาดเสกลเดียวกับ y=Cx เช่นถ้าลู่เข้าหา 0.6 ( y=0.6) และ r เป็น unit step แสดงได้ดังรูป

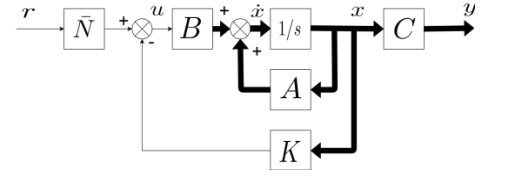
การคำนวณหา \(\bar{N}\) เขียนเป็นสมการอย่างง่ายได้ว่า

\(r\times \bar{N}=y\)

(1)

3)คำนวณหาค่า L โดยคำนวณตาม Ogata

จากรูปที่ 1 จะเห็นว่า system state matrix คือ (A-BK) และ observer state matrix คือ (A-LC) โครงสร้างของทั้งสองเมทริคมีความเหมือนกัน จะแตกต่างกันที่ลำดับการวางตำแหน่งของเมทริคไม่ทราบค่า BK และ LC

จากทฤษฎีเราทราบว่า Eigen value ของ (A-LC) และ (A-LC)^T เหมือนกัน จึงสามารถเขียน observer state matrix ให้มีลำดับการวางของตำแหน่งเช่นเดียวกัน system state matrix ดังนี้

\((A-LC)^{T}=A^{T}-C^{T}L^{T}\)

(2)

สมการ Full state observer แสดงได้ดังนี้

\(\left\{\begin{matrix} \dot{Z}=A^{T}Z+C^{T}v\\ y^{\ast }=B^{T}Z\end{matrix}\right.\)

(3)

เราจึงสามารถใช้วิธีการ Pole placement กับสมการ (3) เช่นเดียวกับ system state matrix (A-BK)

\(|sI-\left ( A^{T}-C^{T}K_{o} \right )|=(s-\mu _{1})\cdots (s-\mu _{n})\)

(4)

โดยที่ \( \mu \) คือตำแหน่งโพลที่ต้องการ ปกติแล้วมักจะออกแบบให้ State Observer มีการตอบสนองเร็วกว่าระบบที่ถูกควบคุม

จากจะสมการ (4) เราพบว่า

\(L=K_{o}^{T}\)

(5)

ทั้งนี้หากระบบเป็นระบบที่สังเกตุได้(Observable) ค่า L จะคำนวณได้เสมอ

คำนวณ Matrix \(A_{o}\) ของ Observer ได้ดังนี้

\(A_{o}=A-LC\)

(6)

นำสมการ (1) – (6) มาทำการจำลองการทำงานโดย Matlab Simulink โดยวางคอนโทรลบล๊อกไดอะแกรมดังภาพ

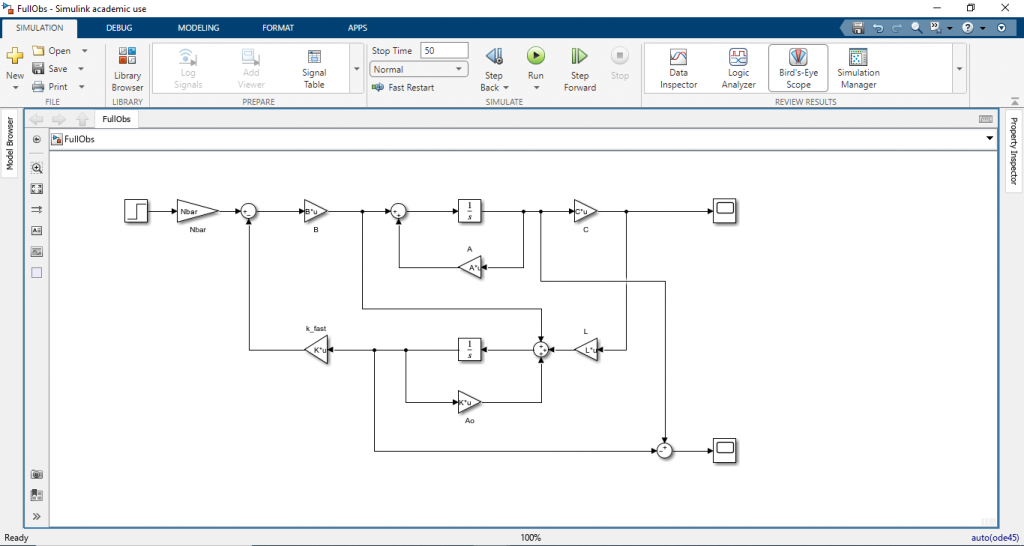
ทำการรันสคริป

syms s

% Define System
A = [0 1 0;245 -0.0814 24.47; 0 0 -250];
B = [0;0;5];
C = [1 0 0];
D = 0;
poles = eig(A)
system_rank=rank(obsv(A,C))


%Step 1. Pole Placement System

p11=-30;
p22=-35;
p33=-45;

K=place(A,B,[p11 p22 p33]);

% Step. 2 Nbar Calculation scale Nbar as y=cx

Nbar=(-C*(A-B*K)^-1*B)^-1;


% Step. 3 Calculation L for Observer

poles=[-5 -6 -7];

L=place(A',C',poles);
L=L'
Ao=A-L*C

open('FullObs.slx')
sim('FullObs.slx')

จะได้ผลลัพธ์ดังนี้