การหาสมการเสตทของลูกตุ้มกลับหัว (Inverted Pendulum) ด้วยวิธีพลังงาน และจำลองระบบโดย Matlab -

นอกจากการใช้กฎข้อที่สองของนิวตันในการหาสมการพลศาสตร์แล้ว ยังมีอีกหนึ่งวิธีที่ใช้กันบ่อย ก็คือการใช้ Lagrange’s equation เขียนในรูปทั่วไปได้ดังนี้

\(\frac{d}{dt}\left ( \frac{\partial L}{\partial \dot{q}_{i}} \right )-\frac{\partial L}{\partial \dot{q}_{i}}=Q_{i}\)

(1)

L คือ Lagrange function แสดงได้ดังนี้

\(L=T(q_{1},\cdots ,q_{r},\dot{q}_{1},\cdots ,\dot{q}_{r})-V(q_{1},\cdots ,q_{r})\)

(2)

T คือฟังชั่นพลังงานจล
V คือฟังชั่นพลังงานศักดิ์
\(Q_{i}\) คือแรงภายนอกที่มากระทำ

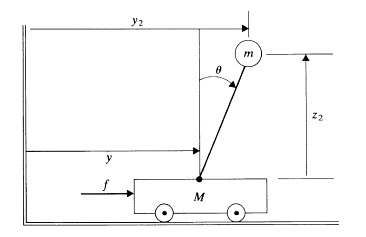
Free body diagram ของ Inverted Pendulum แสดงได้ดังนี้

ฟังชั่นพลังงานจลของ Pendulum เขียนเป็นสมการได้ดังนี้

\(T_{1}=\frac{1}{2}M\dot{y}^{2}\)

(3)

\(T_{2}=\frac{1}{2}m\left ( \dot{y}_{2}^{2}+\dot{z}_{2}^{2} \right )\)

(4)

ระยะการเคลื่อนที่ของมวล m ได้เป็นสมการได้ดังนี้

\(y_{2}=y+lsin\theta\)

(5)

\(\dot{y_{2}}=\dot{y}+l\dot{\theta }cos\theta\)

(6)

\(z_{2}=lcos\theta\)

(7)

\(\dot{z_{2}}=-l\dot{\theta }sin\theta\)

(8)

แทนสมการ (5) – (8) ลงใน (3) – (4)

\(T=T_{1}+T_{2}=\frac{1}{2}M\dot{y}^{2}+\frac{1}{2}m[(\dot{y}+l\dot{\theta }cos\theta)^{2}+l^{2}\dot{\theta }^{2}sin^{2}\theta ]\)

(9)

\(T=\frac{1}{2}M\dot{y}^{2}+\frac{1}{2}m[\dot{y}^{2}+2\dot{y}\dot{\theta }lcos\theta+l^{2}\dot{\theta^{2}}]\)

(10)

ฟังชั่นพลังงานศักดิ์ของระบบ แสดงได้ด้วยสมการ

\(V=mgz_{2}=mglcos\theta\)

(11)

แทน (10) และ (11) ลงใน Lagrange function (2)

\(L=T-V=\frac{1}{2}(M+m)\dot{y}^{2}+mlcos\theta\dot{y}\dot{\theta }+\frac{1}{2}ml^{2}\dot{\theta }^{2}-mglcos\theta\)

(12)

จากรูปที่ 1 เรากำหนด coordinate 2 ตำแหน่ง คือ \(y\) และ \(\theta\) ดังนั้นสามารถเขียน Lagrange equation ได้ดังนี้

\(\frac{d}{dt}\left ( \frac{\partial L}{\partial \dot{y}} \right )-\frac{\partial L}{\partial y}=f\)

(13)

\(\frac{d}{dt}\left ( \frac{\partial L}{\partial \dot{\theta }} \right )-\frac{\partial L}{\partial \theta }=0\)

(14)

แทน (12) ลงใน (13) และ (14) จะได้

\(\frac{\partial L}{\partial \dot{y}}=(M+m)\dot{y}+mlcos\theta \dot{\theta }\)

(15)

\(\frac{\partial L}{\partial y}=0\)

(16)

\(\frac{\partial L}{\partial \dot{\theta }}=mlcos\theta \dot{y}+ml^{2}\dot{\theta }\)

(17)

\(\frac{\partial L}{\partial \theta }=mglsin\theta-mlsin\theta\dot{y}\dot{\theta }\)

(18)

แทนค่า (15) – (18) ลงใน (13) – (14)

\((M+m)\ddot{y}+mlcos\theta \ddot{\theta }-ml\dot{\theta }^{2}sin\theta=f\)

(19)

\(mlcos\theta\ddot{y}+ml^{2}\ddot{\theta }-mglsin\theta=0\)

(20)

ทำการ Linearization รอบจุดสมดุลโดยสมมติว่ามีการเปลี่ยนแปลงเพียงเล็กน้อย \(cos\theta\sim1\) และ \(sin\theta=\theta\) จะได้

\((M+m)\ddot{y}+ml\ddot{\theta }=f\)

(21)

\(m\ddot{y}+ml\ddot{\theta }-mg\theta =0\)

(22)

กำหนดตัวแปรสถานะ (state variable)

\(x=\begin{bmatrix} y \\ \theta\\ \dot{y}\\ \dot{\theta }\end{bmatrix}\)

(23)

จัดรูป (21) และ (22)

\(\frac{dy}{dt}=\dot{y}\)

(24)

\(\frac{d\theta }{dt}=\dot{\theta }\)

(25)

\(\frac{d\dot{y}}{dt}=\frac{f}{M}-\frac{mg}{M}\theta\)

(26)

\(\frac{d\dot{\theta }}{dt}=-\frac{f}{Ml}+\left (\frac{M+m}{Ml} \right )g\theta\)

(27)

สมการเสตทจะอยู่ในรูป

\(\dot{x}=Ax+Bu\)

\(y=Cx\)

\(\dot{x}=\begin{bmatrix} 0&0&1&0\\ 0&0&0&1\\ 0&-mg/M&0&0\\ 0&(M+g)g/Ml&0&0\\ \end{bmatrix}x+\begin{bmatrix} 0\\ 0\\ 1/M\\ -1/Ml\end{bmatrix}f\)

(28)

\(y=\begin{bmatrix} 1&1&0&0\\ \end{bmatrix}\begin{bmatrix} y\\ \theta \\ \dot{y}\\ \dot{\theta }\end{bmatrix}\)

(29)

นำสมการ (28) และ (29) มาเขียนเป้นสคริปบน Matlab ดังนี้

clear;
clc;
close all;


% plant params (physical values)
g = 9.81;  % gravity [m/s^2]
cM = 5;    % Cart mass [kg]
pL = 0.25;  % pendulum length [m]
pm = 1;     % pendulum mass [kg]

% model params -- slightly off to account for non-perfect characterization
cM_model = cM+0.2;
pL_model = pL-0.1; 
pm_model = pm-0.15; 

A = [0                      0                           1	0
     0                      0                           0	1
     0           (-pm_model*g)/cM_model                 0	0
     0	((cM_model+pm_model)*g)/(cM_model*pL_model) 	0	0];
B = [0                          0;
     0                          0;
     1/cM_model                 -1/cM_model;
     -1/(cM_model*pL_model)     (cM_model+pm_model)/(cM_model*pm_model*pL_model)];
C = [1  0  0  0
     0  1  0  0];
D = 0;
sys_cl = ss(A,B,C,D);
fprintf('\nControllability:\n\trank(ctrb(sys))=%d\n',rank(ctrb(sys_cl)));

จะพบว่าระบบมีคุณสมบัตรควบคุมได้ (Controlable) เราจึงสามารถนำสมการเสตทดังกล่าวไปใช้ในการออกแบบระบบควบคุมต่อไป

ดาวน์โหลด Matlab file ได้ที่นี่