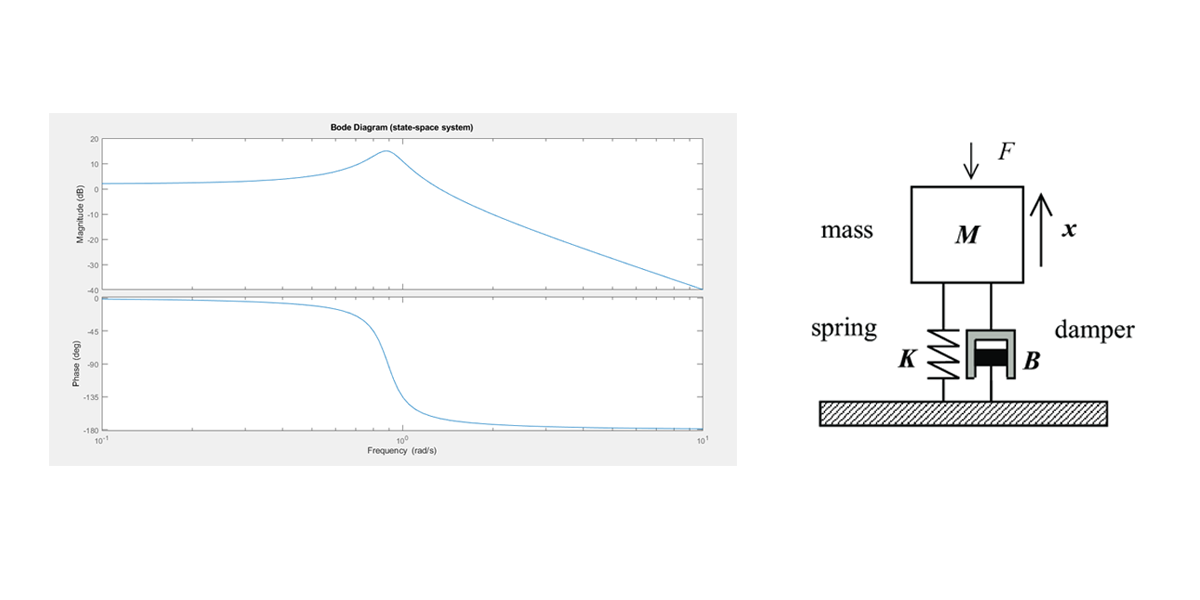
จากที่ได้ศึกษาจากบล๊อก จำลองการทำงานของ Mass spring damped system บล๊อกนี้ขอนำเสนอการ plot ที่จำเป็นเพิ่มเติมต่อการวิคราะห์ระบบ
1) รันสคริปข้อมูลพื้นฐานระบบ mass spring damped system
clear;
close all;
%% Parameters
m = 1; %[kg]
k = 0.8; %[N/m]
c = 0.2; %[Ns/m]
% timestep
dt = 0.001; %[s]
experimentStopTime = 60; %[s]
% frequencies
wmin = 0.1; %[Hz]
wmax = 10; %[Hz]
%% State-space parameter
A = [0 1; -k/m -c/m];
B = [0 1/m]';
C = [1 0];
D = [0];
2) รัน Simulink model ดังนี้

3) รันสคริปเพื่อ plot กราฟผลลัพธ์
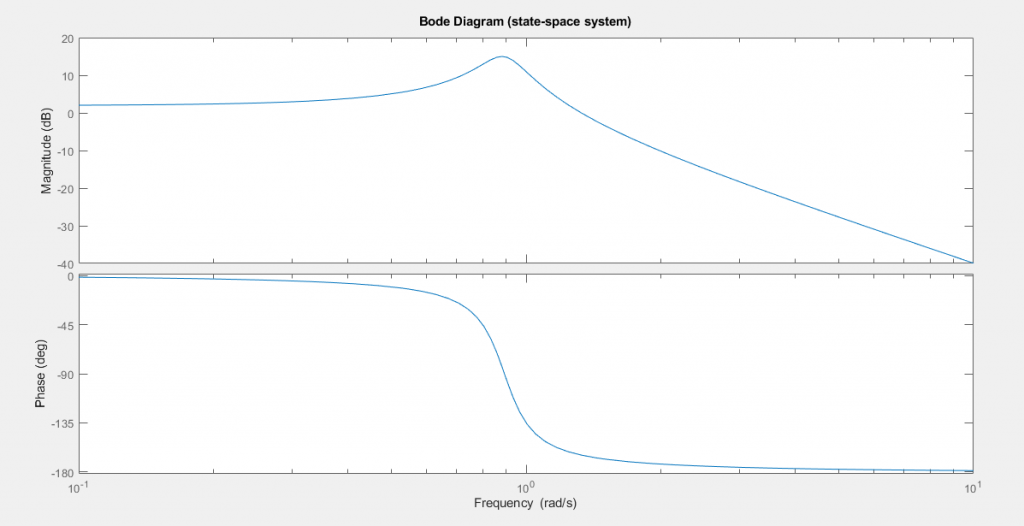
%% State-space system
sys = ss(A,B,C,D);
figure;
bode(sys, {wmin, wmax});
title('Bode Diagram (state-space system)');
%% Physical system
% Time domain
figure;
subplot(2,1,1);
plot(time_sim, x_sim);
ylabel('x (m)');
subplot(2,1,2);
plot(time_sim, F_sim);
ylabel('F (N)');
xlabel('time (sec)');
% Bode Plot
datat=iddata(x_sim, F_sim, dt); % represent the system as input and output
% data with timestep dt (time domain)
dataf=fft(datat); % same data in the frequency domain
set(dataf,'InputName','F', 'OutputName', 'x')
gf=spafdr(dataf); % estimate frequency response using spectral analysis
figure;
bode(gf, {wmin, wmax});
title('Bode Diagram (simulation)');
% Estimate transfer function
% Of the form: X/F = 1/(m*s^2 + c*s + k)
np = 2;
nz = 0;
fprintf('\nEstimating transfer function....\n');
sysest = tfest(dataf, np, nz)
ดาวน์โหลดไฟล์ได้ที่นี่