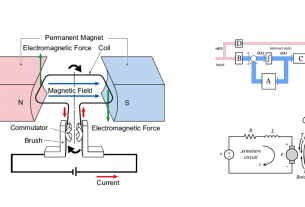
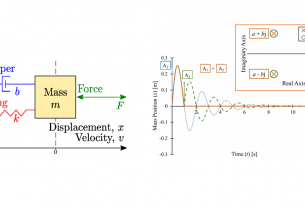
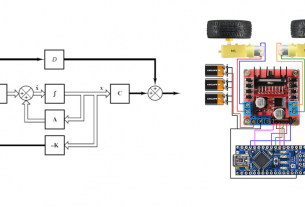
การศึกษาระบบควบคุมระดับน้ำในถังที่เชื่อมต่อกัน เริ่มต้นที่การศึกษาแบบจำลองของระบบรักษาระดับน้ำถังเดียว แสดงดังรูปที่ 1
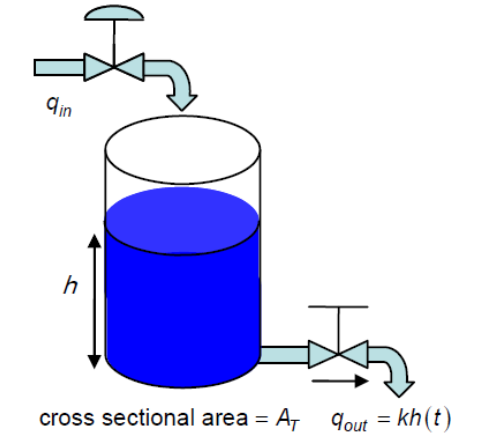
อัตราการไหลออกของของไหลแสดงได้ด้วยสมการ
(1)
โดยที่ \(k\) เป็นค่าคงที่
สมการสมดุลมวลของระบบถังเดียวเขียนได้ดังนี้
(2)
โดยที่ \(V(t)\) คือปริมาตรของของไหล
จัดรูปสมการ (2) จะได้
(3)
แทนค่า \(q_{out}\)
(4)
จัดรูปสมการ (4) จะได้สมการพลศาสตร์ของระบบถังที่ 1
(5)
ต่อมาพิจารณาหาสมการพลศาสตร์ของถังที่ 2 ดังแสดงในภาพที่ 2
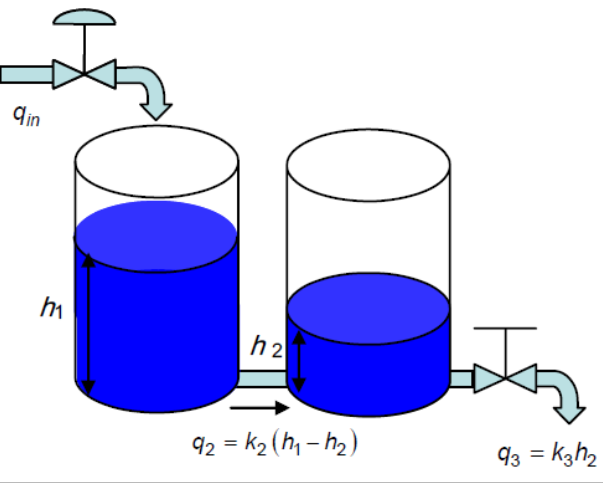
สมการสมดุลมวลของระบบถังที่สองเขียนได้ดังนี้
(6)
สมการ (5) และ (6) เขียนในรูปสมการเสตท ได้ดังนี้
(7)
กำหนดให้
\(A_{1}=A_{2}\)= 32 cm^2
\(k_{2}=k_{3}\)=14.3
แทนค่าลงในสมการ (7) จะได้
(8)
นำสมการ (8) ไปสร้างเป็น control block diagram บนโปรแกรม Simulink ดังนี้
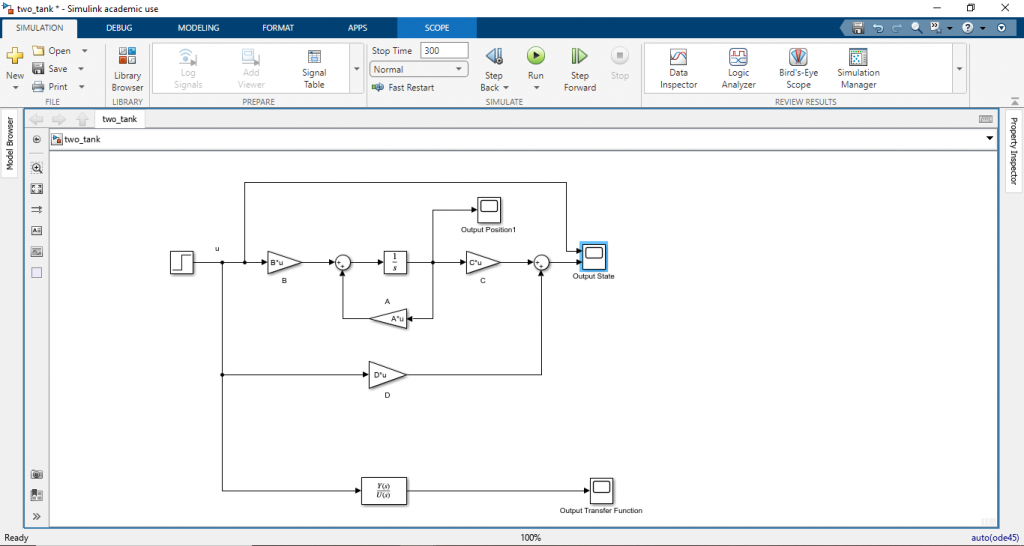
ทำการรันสคริปดังนี้
%%state model
A=[-0.4469 0.4469; 0.4469 -0.8938];
B=[0.03125;0];
C=[0 1];
D=[0];
%%check controlable
p=ctrb(A,B);
rankp=rank(p)
%%check observable
q=obsv(A,C);
rankq=rank(q)
%creat transfer function
[num1,den1]=ss2tf(A,B,C,D,1)
open("two_tank.slx")
sim('two_tank.slx')
จะได้ผลลัพธ์การจำลองการทำงาน ซึ่งจะพบว่าผลตอบสนองของระบบยังไม่ลู่เข้าสู่ค่า Set Point ทั้งนี้เพราะยังมิได้มีการเพิ่มตัวควบคุมที่เหมาะสมให้แก่ระบบ ดังนี้
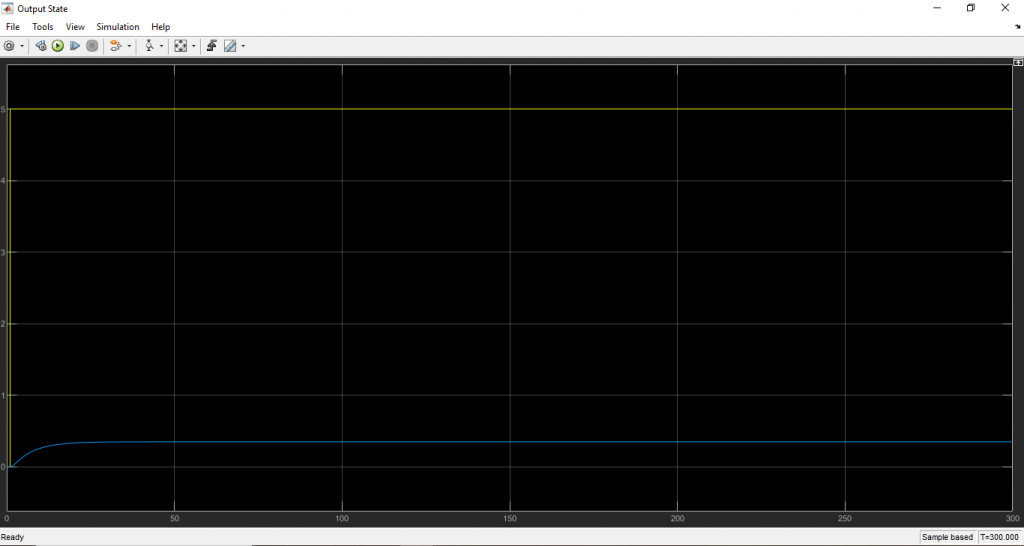
ดาวน์โหลด Matlab/Simulink file ได้ทีนี่