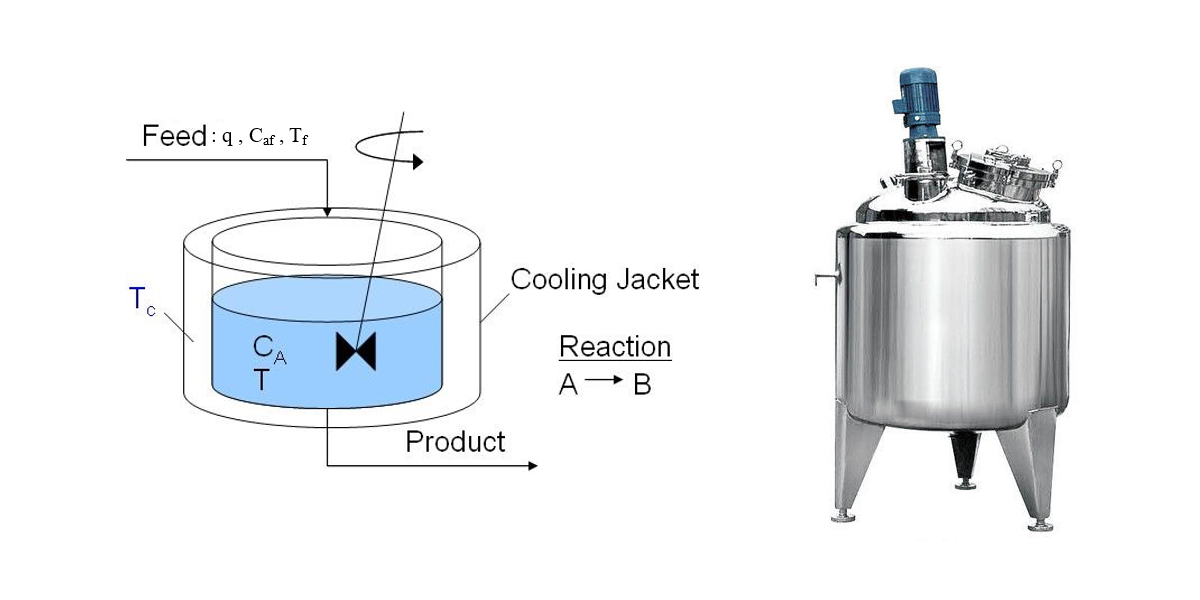
ถังกวนแบบปฏิกิริยาต่อเนื่อง หรือ Continuous Stirred Tank Reactor (CSTR) เป็นภาชนะเพื่อทำปฏิกิริยา ระหว่างตัวทำปฏิกิริยา และตัวทำละลาย โดยให้ตัวทำละลายไหลเข้าไปในถังในขณะที่ผลิตภัณฑ์ของปฏิกิริยาไหลออกจากถัง
ถังกวนแบบปฏิกิริยาต่อเนื่อง Continuous Stirred Tank Reactor (CSTR) พบมากในอุตสาหกรรม การควบคุมเพื่อให้ได้ผลลัพธ์ตามกำหนดต้องมีความเข้าใจสมการพลศาสตร์ของระบบ ในบล็อกนี้เราจะศึกษาแบบจำลองโดยอ้างอิงจาก หนังสือ Process Dynamics: Modeling, Analysis and Simulation สำนักพิมพ์ Prentice-Hall
ถังกวนแบบปฏิกิริยาต่อเนื่องแสดงได้ดังรูปที่ 1
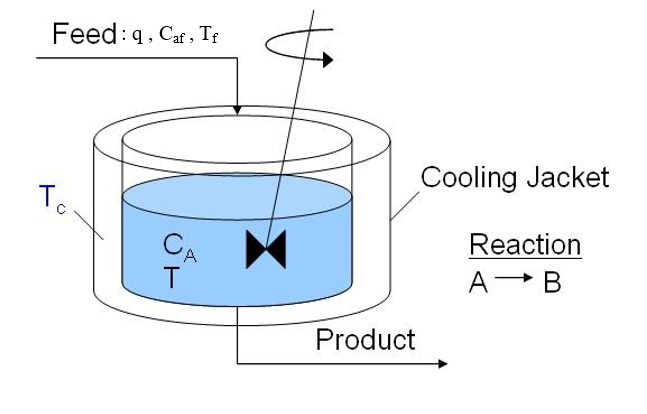
การสร้างแบบจำลองของถังกวนแบบปฏิกิริยาต่อเนื่อง เราจะสมมติว่าการผสมเกิดขึ้นอย่างสมบูรณ์ (perfect mixed) เป็นกระบวนการผันกลับไม่ได้(irreversible) และจำลองระบบโดยสมการอนุพันธ์อันดับหนึ่ง
จากหนังสือ Process Dynamics ความเข้มข้นของตัวทำปฏิกิริยาภายในถังสามารถแสดงได้โดยสมการ
(1)
อัตราการเกิดปฏิกิริยาภายในถัง โดย Arrhenius rate law เขียนเป็นสมการได้ดังนี้
(2)
จากการสมดุลพลังงาน จะได้อัตราการเปลี่ยนแปลงอุณหภูมิของปฏิกิริยาดังนี้
(3)
ถังกวนแบบปฏิกิริยาต่อเนื่อง มี 1 อินพุต
Tc อุณหภูมิห่อหุ้มถัง (Jacket temperature) (K)
และมี 2 เอาพุต
Ca ความเข้มข้นของสาร A ภายในถัง (kgmol/m^3)
T อุณหภูมิของการเกิดปฏิกิริยา (K)
มีพารามิเตอร์ที่ต้องกำหนดค่าดังนี้
Caf ความเข้มข้นของสาร A ที่ไหลเข้าสู่ถัง (kgmol/m^3)
Tf อุณหภูมิของสาร A ที่ไหลเข้าสู่ถัง (K)
q อัตราการไหลเชิงปริมาตร (volume/time) (m^3/h)
V ปริมาตรของถัง (m^3)
k0 Pre-exponential nonthermal factor (1/h)
E ค่าพลังงานก่อกัมมันต์ (Activation Energy) (kcal/kgmol)
R ค่าคงที่ของ (kcal/(kgmol*K) )
H ค่าปฏิกิริยาความร้อน (kcal/kgmol)
rho ค่าความหนาแน่นของของผสม A-B Mixture (kg/m^3)
Cp ค่าความจุความร้อน A-B Mixture (J/kg-K)
mdelH ค่าปฏิกิริยาความร้อน A->B (J/mol)
U สัมประสิทธิการถ่ายโอนความร้อนโดยรวม (W/m^2-K)
A พื้นที่เฉพาะส่วนที่คำนวนณ U (m^2)
ในการจำลองการทำงาน เราจะใช้ Unit Step Input โดยการลดอุณหภูมิของ Jacket (Tc) แบบทันที จากอุณหภูมิเริ่มต้น 324 K เป็น 290 K และแก้สมการ (1) (2) และ (3) เพื่อหาผลตอบสนองของระบบโดยใช้ Matlab Script
สร้างสคริป cstr1.m เพื่อใช้ในการคำนวณสมการ (1) (2) และ (3) ดังนี้
% CSTR model from
%
% Michael A. Henson and Dale E. Seborg. Nonlinear Process Control.
% Prentice Hall PTR, Upper Saddle River, New Jersey, 1997.
% Description:
% Continuously Stirred Tank Reactor with energy balance and reaction A->B.
% The temperature of the cooling jacket is the control.
function xdot=cstr1(t,x)
global u
% Input (1):
% Temperature of cooling jacket (K)
Tc = u;
% States (2):
% Concentration of A in CSTR (mol/m^3)
Ca = x(1,1);
% Temperature in CSTR (K)
T = x(2,1);
% Parameters:
% Volumetric Flowrate (m^3/sec)
q = 100;
% Volume of CSTR (m^3)
V = 100;
% Density of A-B Mixture (kg/m^3)
rho = 1000;
% Heat capacity of A-B Mixture (J/kg-K)
Cp = .239;
% Heat of reaction for A->B (J/mol)
mdelH = 5e4;
% E - Activation energy in the Arrhenius Equation (J/mol)
% R - Universal Gas Constant = 8.31451 J/mol-K
EoverR = 8750;
% Pre-exponential factor (1/sec)
k0 = 7.2e10;
% U - Overall Heat Transfer Coefficient (W/m^2-K)
% A - Area - this value is specific for the U calculation (m^2)
UA = 5e4;
% Feed Concentration (mol/m^3)
Caf = 1;
% Feed Temperature (K)
Tf = 350;
% Compute xdot:
xdot(1,1) = (q/V*(Caf - Ca) - k0*exp(-EoverR/T)*Ca);
xdot(2,1) = (q/V*(Tf - T) + mdelH/(rho*Cp)*k0*exp(-EoverR/T)*Ca + (UA/(V*rho*Cp))*(Tc-T));
ทำการสร้าง และรันสคริป step.m เพื่อส่งอินพุทไปยังฟังชั่น cstr1.m และทำการพล๊อตกราฟผลตอบสนองดังนี้
% Step test for Model 1 - CSTR
global u
% State Initial Conditions
Ca_ss = 0.877;
T_ss = 324.475;
x_ss = [Ca_ss;T_ss];
% Open Loop Step Change in Jacket Temperature
u = 290;
% Final Time (sec)
tf = 5;
[t,x] = ode15s('cstr1',[0 tf],x_ss);
% Parse out the state values
Ca = x(:,1);
T = x(:,2);
% Plot the results
figure(1);
plot(t,Ca);
title('Concentration')
legend('Concentration Change in CSTR')
figure(2);
plot(t,T);
title('Temperature')
legend('Temperature Change in CSTR')
จะได้ผลลัพธ์ดังนี้
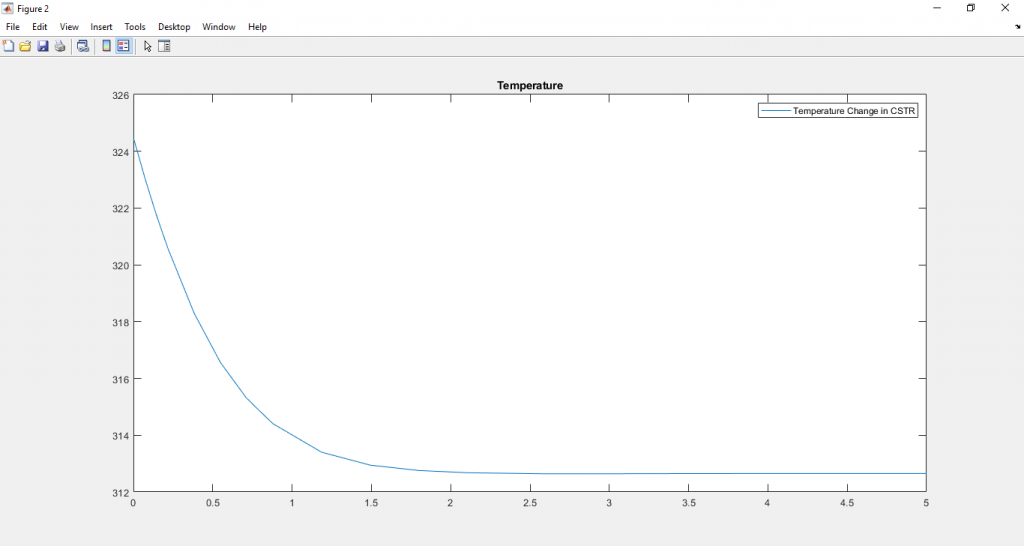
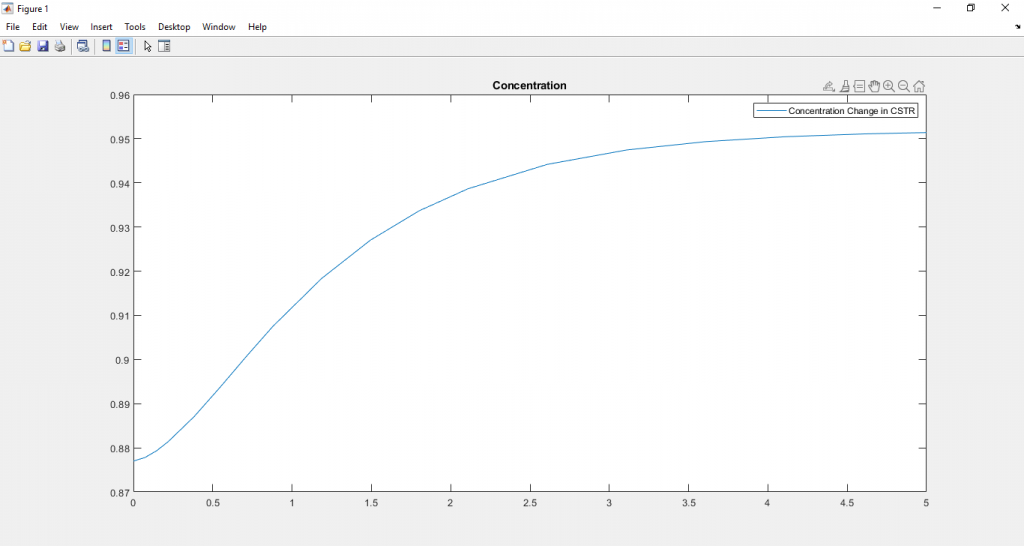
ดาวน์โหลดไฟล์ Matlab ได้ที่นี่