ระบบทางวิศวกรรมจำนวนมากสามารถประมาณผลการตอบสนองด้วยสมการอนุพันธ์อันดับหนึ่ง ซึ่งสามารถเขียน Laplace Transform Control block diagram ได้ดังนี้

จากบล๊อกไดอะแกรม เราสามารถจัดรูปสมการ Transfer Function ได้เป็น
(1)
แทนค่า \(G(s)\) ด้วยสมการอนุพันธ์อันดับหนึ่งของระบบที่เราสนใจ
จัดรูปสมการ (1) ใหม่จะได้
(2)
ในที่นี้เราจะทดสอบระบบด้วย Unit step input ดังนั้น R(s) สามารถเขียนในรูปของ Laplace Transform ได้ดังนี้
จัดรูปสมการ (2) จะได้
(3)
ทำการ partial faction สมการ (3) สามารถจัดรูปสมการใหม่ได้เป็น
(4)
จากการเปรียบเทียบค่าสัมประสิทธิของสมการที่ (4) ทำให้เราทราบว่า A=1 และ B=-T
แทนค่า A และ B เราจะได้
(5)
ทำการ Inverse Laplace สมการที่ (5) เราจะได้สมการผลตอบสนองของระบบต่อ Unit step input ในโดเมนของเวลาดังนี้
(6)
จากสมการผลตอบสนองของระบบ เราจึงเห็นว่า c(t) จะลู่เข้าหาค่า 1 แต่ในทางปฏิบัติระบบอาจจะลู่เข้าหาค่าอื่นๆ ดังนั้นในการจำลองการทำงานของระบบเราจะเพิ่มค่า K เรียกว่า DC Gain ลงใน Transfer function ของระบบในสมการที่ (2)
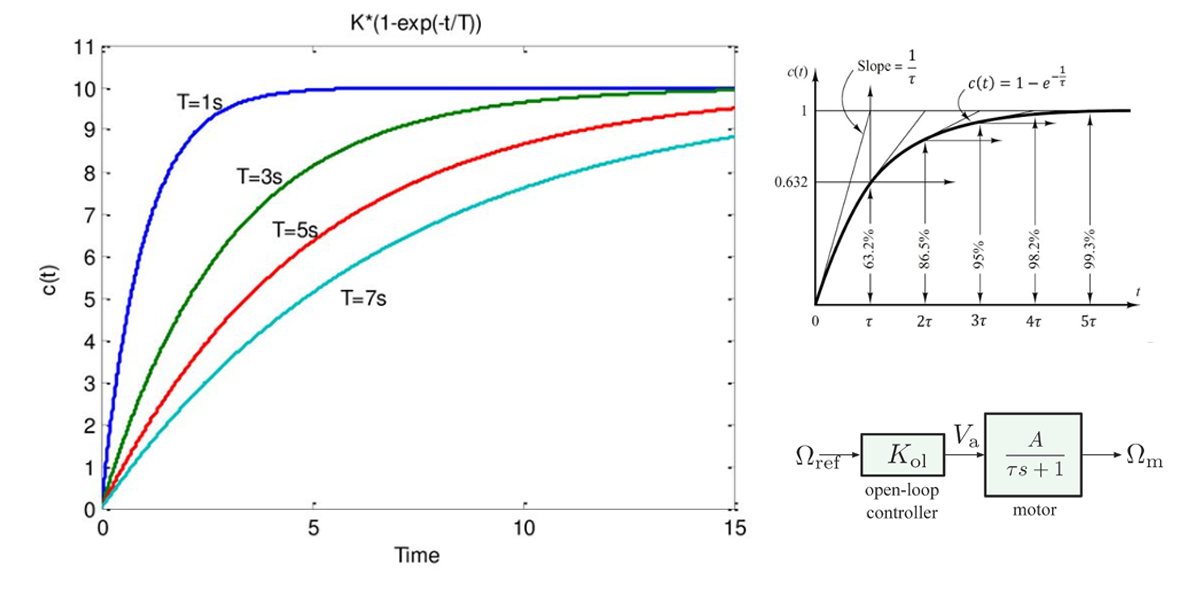
ค่า T ที่ได้จากการจัดรูปสมการคือค่า Time constant ของระบบ เป็นค่าที่จะใช้ประมาณการว่าระบบของจะลู่เข้าสู่ 63% ของผลตอบสนองในช่วงอยู่ตัว(steady state) ที่เวลาเท่าใด
(7)
ในทางทฤษฎีเราสามารถ plot graph ผลตอบสนองของระบบตามสมการที่ (6) ต่อค่า Time Constant ได้ดังนี้

เราจะนำสมการ (7) Transfer Function ของระบบพลศาสตร์ที่มีสมการอนุพันธ์อันดับหนึ่ง ไปจำลองการทำงานในโปรแกรม Matlab/Simulink โดยสมมติว่าระบบที่เราสนใจศึกษาเป็นระบบที่มีอนุพันธ์อันดับหนึ่ง และเมื่อจัดรูปสมการของระบบแล้วจะมีค่า K=5 และค่า Time Constant(T) = 0.05 และป้อน Unit step input ให้แก่ระบบ
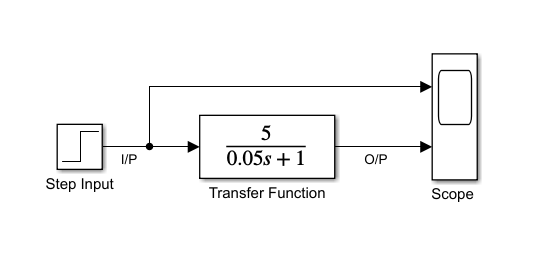
จากการจำลองการทำงานเราจะได้กราฟผลตอบสนองดังนี้

จาการ simulation ทำให้เราทราบว่าระบบจะลู่เข้าสู่ 63.2% ของค่า Final value ที่เวลาน้อยกว่า 0.05 Sec.
สำหรับผู้สนใจสามารถดาวน์โหลด simulink file เพื่อนำไปศึกษาได้ที่นี้