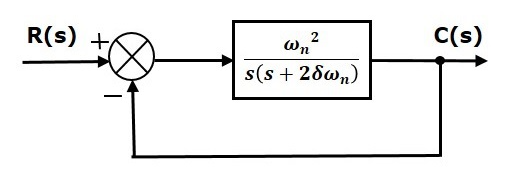
ระบบพลศาสตร์จำนวนมากสามารถประมาณการผลตอบสนองของระบบโดยใช้สมการเชิงอนุพันธ์อันดับสอง และสามารถเขียนเป็น Laplace Transform Block diagram ได้ดังนี้
Transfer function ของระบบป้อนกลับตามรูปข้างต้นสามารถเขียนได้เป็น
\(\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}\)
เมื่อพิจารณาจาก Close Loop Block diagram ข้างต้นพบว่า G(s) สามารถเขียนได้เป็น
\(G(s)=\frac{\omega _{n}^{2}}{s\left ( s+2\delta \omega _{n} \right )}\)
แทนสมการ (2) ลงใน สมการ (1) และทำการจัดรูปจะได้ Close Loop Transfer function
\(\frac{C(s)}{R(s)}=\frac{\omega _{n}^{2}}{s^{2}+2\delta \omega _{n}s+\omega _{n}^{2}}\)
จากสมการ (3) เราจะเรียกเทอมส่วนว่า Characteristic equation สมการ (4) โดยรากของสมการจะเป็นเป็นตัวกำหนดคุณลักษณะการตอบสนองของระบบพลศาสตร์ต่ออินพุตที่เข้ามากระทำ
\({s^{2}+2\delta \omega _{n}s+\omega _{n}^{2}}=0\)
พิจารณาผลตอบสนองของระบบต่อ Step input ดังนั้น จะสามารถเขียน R(s) ได้เป็น
แทนสมการ (5) Step Input ลงในสมการ Transfer function (3) สามารถจัดแบ่งการตอบสนองของระบบออกได้เป็น 4 กรณี ดังนี้
จัดรูปสมการ (3) และ สมการ (5) จะได้
\(\frac{C(s)}{R(s)}=\frac{\omega _{n}^{2}}{s^{2}+\omega _{n}^{2}}\)
ทำการป้อน Step input ให้แก่สมการ (6) จะได้
\(C(s)=\frac{\omega _{n}^{2}}{s^{2}+\omega _{n}^{2}}R(s)\)
\(C(s)=\frac{\omega _{n}^{2}}{s^{2}+\omega _{n}^{2}}\left ( \frac{1}{s} \right )=\frac{\omega _{n}^{2}}{s\left ( s^{2}+\omega _{n}^{2} \right )}\)
ทำการ Inverse Laplace สมการ (7) จะได้สมการผลตอบสนองบนโดเมนเวลา เป็น
\(c(t)=\left ( 1-cos(\omega _{n}t) \right )u(t)\)
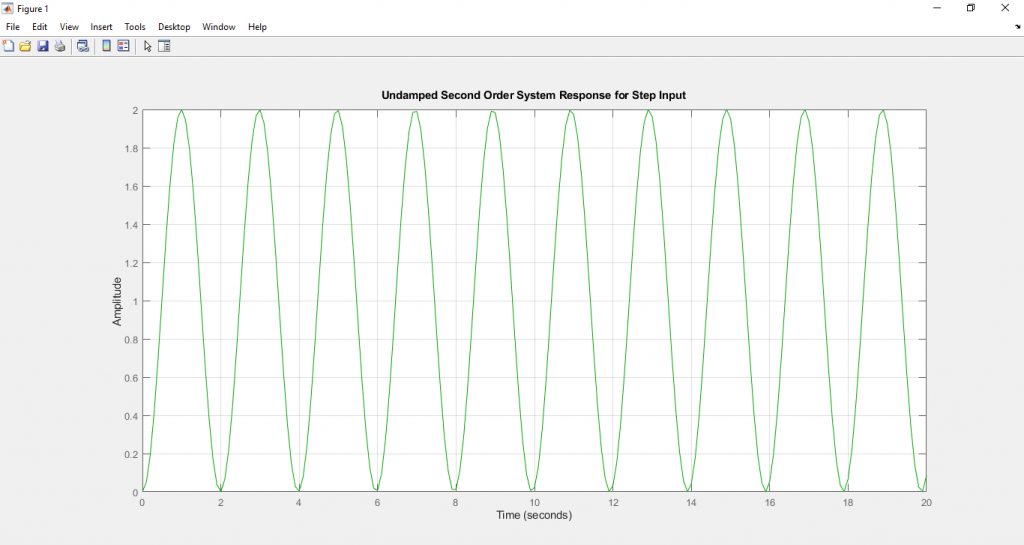
จากสมการ (8) พบว่า ผลตอบสนองของระบบต่อ Unit step input จะเป็นสัญญาณที่มีความต่อเนื่อง มีขนาด ของสัญญาณ (amplitude) และ ความถี่ (frequency) คงที่
เราจะทดลองนำสมการ (6) ไปทำการจำลองการทำงาน โดยโปรแกรม Matlab และให้ G(s) เป็นดังนี้
\(G(s)=\frac{10}{s^{2}+10}\)
และมี Matlab script ดังนี้
num=[10]
den=[1 0 10]
t=0:0.1:20
sys=tf(num,den)
step(sys,t,'g')
title('Undamped Second Order System Response for Step Input')
grid on
stepinfo(sys)
เราสามารถจำลองการทำงานโดยนำ script ข้างต้นไปวางบน Command window ของโปรแกรม Matlab
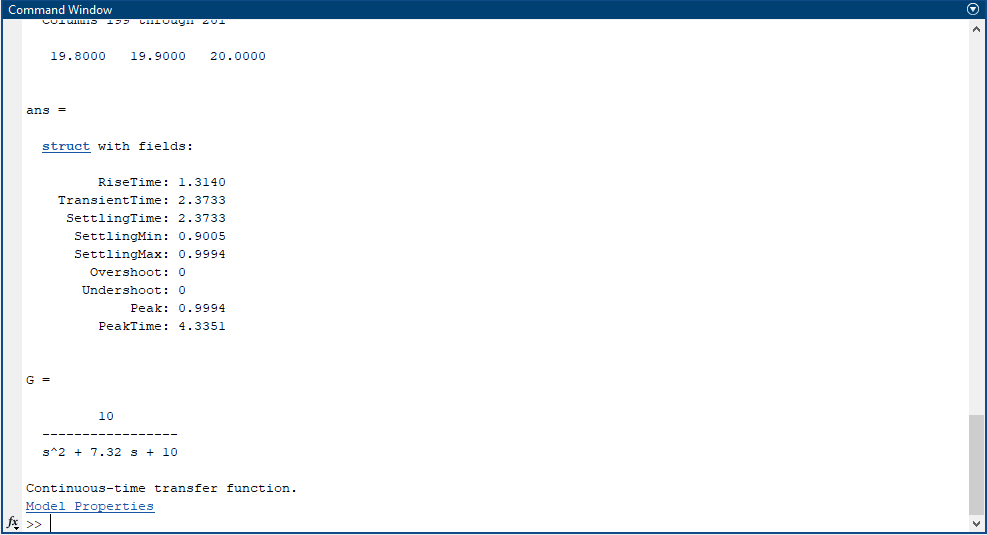
เนื่องจากระบบเป็น undamped จึงไม่มีค่า Rise time , Settling time , Over shoot , Peak time และมีค่า Natural frequency = 3.16 rad/s
Case 2 : Critically Damped System
จากสมการ (3) สามารถเขียนใหม่ได้เป็น
\(\frac{C(s)}{R(s)}=\frac{\omega _{n}^{2}}{s^{2}+2\cdot 1\cdot \omega _{n}s+\omega _{n}^{2}}\)
จัดรูปสมการ (9) และ สมการ (5) จะได้
\(C(s)=\left ( \frac{\omega _{n}^{2}}{\left ( s+\omega _{n}^{2} \right )} \right )R(s)\)
ทำการป้อน Unit step input ให้แก่สมการ (10) และจัดรูปใหม่จะได้
\(C(s)=\left ( \frac{\omega _{n}^{2}}{\left ( s+\omega _{n}^{2} \right )} \right )\left ( \frac{1}{s} \right )=\frac{\omega _{n}^{2}}{s\left ( s+\omega _{n} \right )^{2}}\)
ทำการ partial fraction สมการ (11) จะได้
\(C(s)=\frac{\omega _{n}^{2}}{s\left ( s+\omega _{n} \right )^{2}}=\frac{A}{s}+\frac{B}{s+\omega _{n}}+\frac{C}{\left ( s+\omega _{n} \right )^{2}}\)
จากการเปรียบเทียบสัมประสิทธิทำให้เราทราบว่า \(A=1, B=-1 , C=-\omega _{n}\)
ทำการแทนค่าที่ได้จากการเปรียบเทียบสัมประสิทธิลงในสมการ (12) จะได้ว่า
\(C(s)=\frac{\omega _{n}^{2}}{s\left ( s+\omega _{n} \right )^{2}}=\frac{1}{s}-\frac{1}{s+\omega _{n}}-\frac{\omega _{n}}{\left ( s+\omega _{n} \right )^{2}}\)
ทำการ Inverse Laplace สมการ (13) จะได้สมการผลตอบสนองของระบบ ในโดเมนเวลาดังนี้
\(c(t)=(1-e^{-\omega _{n}t}-\omega _{n}te^{-\omega _{n}t})u(t)\)
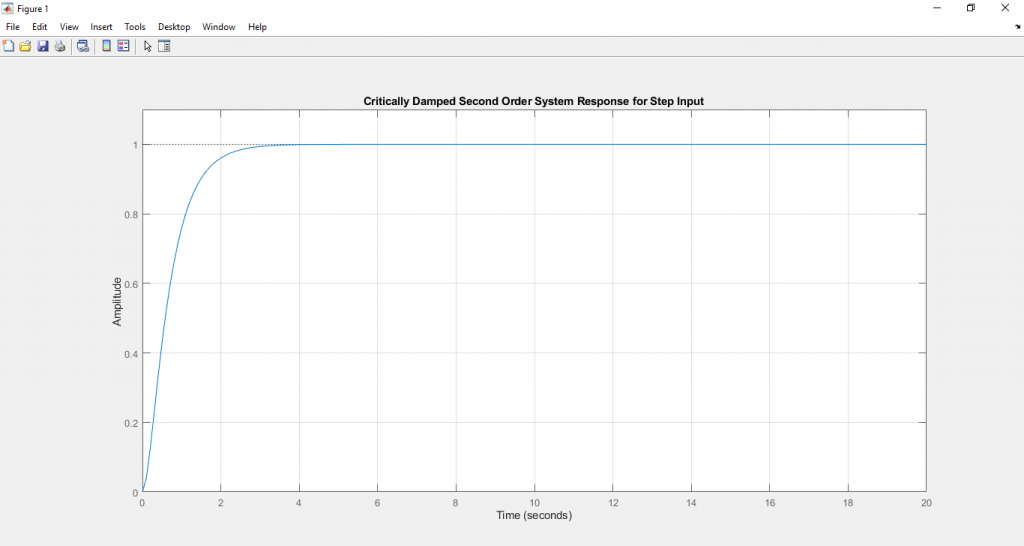
พิจารณาสมการ (14) เราจะพบว่า ผลตอบสนองของระบบจะพยามลู่เข้าหา Step input ในช่วง Steady state
เราจะนำสมการ (9) ไปทำการ simulation บน Matlab โดยกำหนดค่า ให้แก่ Transfer function ดังนี้
\(G(s)=\frac{10}{s^{2}+7.32s+10}\)
และมี Matlab script ดังนี้
num=[10]
den=[1 7.32 10]
sys=tf(num,den)
t=0:0.1:20
step(sys,t)
title('Critically Damped Second Order System Response for Step Input')
grid on
stepinfo(sys)
G=tf(num,den)
[Wn Z P] = damp(G);
Wn=Wn(1);
Z=Z(1);
เราสามารถจำลองการทำงานโดยนำ script ข้างต้นไปวางบน Command window ของโปรแกรม Matlab
Case 3 : Under Damped System
ทำการจัดรูปเทอมส่วนของสมการ (3) ดังนี้
\(s^{2}+2\delta \omega _{n}s+\omega _{n}^{2}=\left \{ s^{2}+2(s)(\delta \omega _{n})+(\delta\omega _{n})^{2}+\omega _{n}^{2}-(\delta\omega _{n})^{2} \right \}
=(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})\)
จากสมการ (15) เราสามารถเขียน Transfer function ได้เป็น
\(\frac{C(s)}{R(s)}=\frac{\omega _{n}^{2}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})}\)
\(C(s)=\left (\frac{\omega _{n}^{2}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})} \right )R(s)\)
ทำการป้อน Unit step input ให้แก่ระบบ จะได้สมการ
\(C(s)=\left (\frac{\omega _{n}^{2}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})} \right )\frac{1}{s}\)
\(C(s)=\frac{\omega _{n}^{2}}{s((s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2}))}\)
ทำการ Partial faction สมการ (17) จะได้
\(C(s)=\frac{A}{S}+\frac{Bs+C}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})}\)
จากการเปรียบเทียบสัมประสิทธิทำให้เราทราบว่า \(A=1, B=-1 , C=-2\delta \omega _{n}\)
แทนค่าสัมประสิทธิกลับลงในสมการ (18)
\(C(s)=\frac{1}{S}-\frac{s+2\delta \omega _{n}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})}\)
\(C(s)=\frac{1}{s}-\frac{s+\delta _{n}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})}-\frac{\delta\omega _{n}}{(s+\delta \omega _{n})^{2}+\omega _{n}^{2}(1-\delta ^{2})}\)
\(C(s)=\frac{1}{s}-\frac{(s+\delta _{n})}{(s+\delta \omega _{n})^{2}+(\omega _{n}\sqrt{1-\delta ^{2}})^{2}}-\frac{\delta }{\sqrt{1-\delta ^{2}}}\left ( \frac{\omega _{n}\sqrt{1-\delta ^{2}}}{(s+\delta \omega _{n})^{2}+(\omega _{n}\sqrt{1-\delta ^{2}})^{2}}\right )\)
กำหนดตัวแปร damping frequency แทนลงใน (19)
\(\omega_{d}=\omega_{n}\sqrt{1-\delta ^{2}}\)
จัดรูปสมการ (19) ใหม่ จะได้
\(C(s)=\frac{1}{s}-\frac{(s+\delta _{n})}{(s+\delta \omega _{n})^{2}+\omega _{d}^2}-\frac{\delta }{\sqrt{1-\delta ^{2}}}\left ( \frac{\omega _{n}\sqrt{1-\delta ^{2}}}{(s+\delta \omega _{n})^{^{2}}+\omega _{d}^{2}}\right )\)
ทำการ Inverse Laplace สมการ (20)
\(c(t)=\left ( 1-e^{-\delta \omega _{n}t}cos(\omega _{d}t) -\frac{\delta }{\sqrt{1-\delta ^{2}}}e^{-\delta \omega _{n}t}sin(\omega _{d}t)\right )u(t)\)
\(c(t)=\left ( 1-\frac{e^{-\delta \omega _{n}t}}{\sqrt{1-\delta ^{2}}}\left ( (\sqrt{1-\delta ^{2}})cos(\omega _{d}t) +\delta sin(\omega _{d}t)\right ) \right )u(t)\)
กำหนดให้ \( \sqrt{1-\delta ^{2}}=sin\theta \) จะได้
แทน สมการ (22) ลงใน สมการ (21) และทำการจัดรูป c(t) ใหม่
\(c(t)=\left ( 1-\frac{e^{-\delta \omega _{n}t}}{\sqrt{1-\delta ^{2}}}\left ( sin\theta cos(\omega _{d}t)+cos\theta sin(\omega _{d}t) \right ) \right )u(t)\)
\(c(t)=\left ( 1-\left ( \frac{e^{-\delta \omega _{n}t}}{\sqrt{1-\delta ^{2}}}sin(\omega _{d}t+\theta ) \right ) \right )u(t))\)
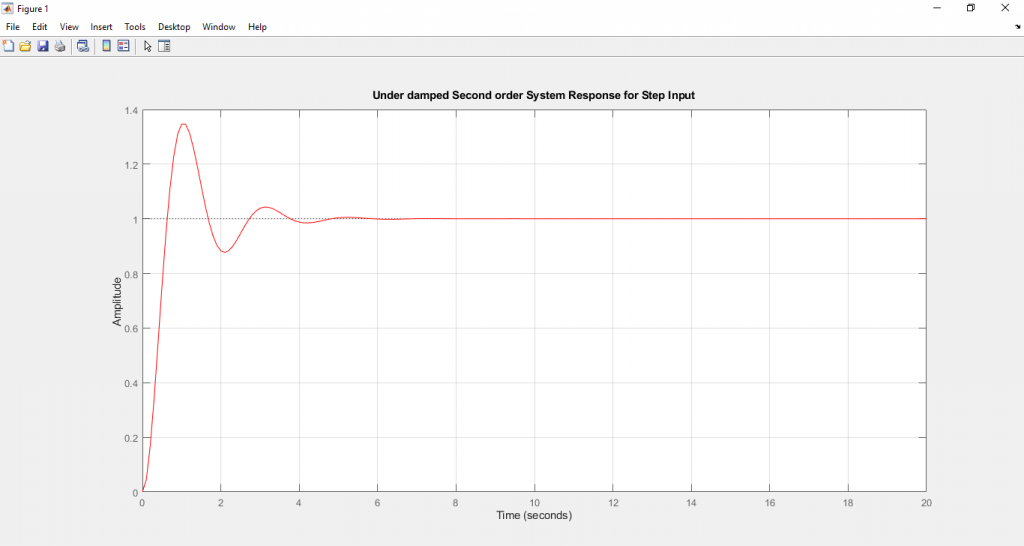
จากสมการ (23) จะพบว่าระบบจะมีลักษณะลู่เข้าสู่สัญญาณ Unit step input มีการ Osilation ตาม damping frequency แต่ Amplitude ของการ Osciltion จะมีขนาดเล็กลงเมื่อเวลาผ่านไป
เราจะนำสมการ (16) ไปทำการ simulation บน Matlab โดยกำหนดค่า ให้แก่ Transfer function ดังนี้
\(G(s)=\frac{10}{s^{2}+2s+10}\)
และมี Matlab script ดังนี้
num=[10]
den=[1 2 10]
sys=tf(num,den)
t=0:0.1:20
[Wn Z P]=damp(sys)
Wn=Wn(1)
Z=Z(1)
step(sys,t,'r')
title('Under damped Second order System Response for Step Input')
grid on
stepinfo(sys)
เราสามารถจำลองการทำงานโดยนำ script ข้างต้นไปวางบน Command window ของโปรแกรม Matlab
Case 4 : Over Damped System
ทำการจัดรูปเทอมส่วนของสมการ (3) ดังนี้
\(s^{2}+2\delta \omega _{n}s+\omega _{n}^{2}=\left \{ s^{2}+2(s)(\delta \omega _{n})+(\delta\omega _{n})^{2}+\omega _{n}^{2}-(\delta\omega _{n})^{2} \right \}
=(s+\delta \omega _{n})^{2}-\omega _{n}^{2}(\delta ^{2}-1)\)
จากสมการ (24) จะได้ Transfer Function
\(\frac{C(s)}{R(s)}=\frac{\omega _{n}^{2}}{(s+\delta\omega_{n})^{2}-\omega_{n}^{2}(\delta ^{2}-1)}\)
\(C(s)=\left ( \frac{\omega _{n}^{2}}{(s+\delta\omega_{n})^{2}-\omega_{n}^{2}(\delta ^{2}-1)} \right )R(s)\)
ทำการป้อน Unit step input
\(C(s)=\left ( \frac{\omega _{n}^{2}}{(s+\delta\omega_{n})^{2}-\omega_{n}^{2}(\delta ^{2}-1)} \right )\frac{1}{s}\)
จัดรูปสมการ (26)
\(C(s)=\left ( \frac{\omega _{n}^{2}}{(s+\delta\omega_{n})^{2}-(\omega_{n}\sqrt{\delta ^{2}-1})^{2}} \right )\frac{1}{s}\)
\(C(s)=\frac{\omega _{n}^{2}}{s(s+\delta\omega_{n}+\omega _{n}\sqrt{\delta ^{2}-1})(s+\delta\omega_{n}-\omega _{n}\sqrt{\delta ^{2}-1}) }\)
ทำการ Partial fraction สมการ (27)
\(C(s)=\frac{A}{s}+\frac{B}{s+\delta\omega_{n}+\omega _{n}\sqrt{\delta ^{2}-1}}+\frac{C}{s+\delta\omega_{n}-\omega _{n}\sqrt{\delta ^{2}-1} }\)
เทียบสัมประสิทธิสมการ (28) ทำให้เราทราบว่า
\(B=\frac{1}{2(\delta +\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}\)
\(C=\frac{-1}{2(\delta -\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}\)
แทนค่า A, B และ C กลับลงในสมการ (28) จะได้
\(C(s)=\frac{1}{s}+\frac{1}{2(\delta +\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}\left (\frac{1}{s+\delta\omega_{n}+\omega _{n}\sqrt{\delta ^{2}-1}} \right )-\frac{1}{2(\delta -\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}\left (\frac{1}{s+\delta\omega_{n}-\omega _{n}\sqrt{\delta ^{2}-1} } \right )\)
ทำการ InverseLaplace สมการ (29)
\(C(t)=\left ( 1+\frac{1}{2(\delta +\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}e^{-(\delta\omega _{n}+\omega _{n}\sqrt{\delta ^{2}-1})t}-\frac{1}{2(\delta -\sqrt{\delta ^{2}-1})(\sqrt{\delta ^{2}-1})}e^{-(\delta\omega _{n}-\omega _{n}\sqrt{\delta ^{2}-1})t} \right )u(t)\)
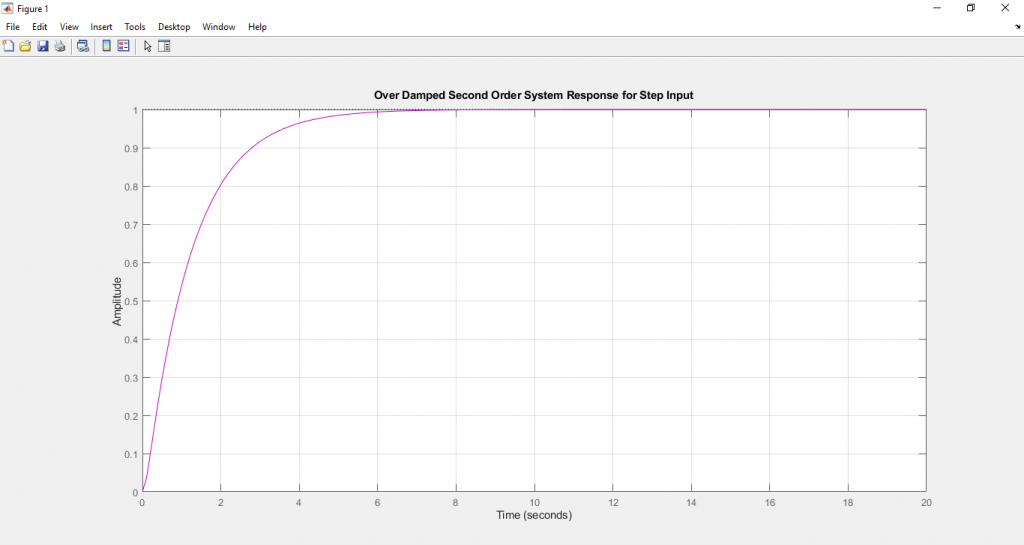
จากสมการ (30) เราจะพบว่า ผลตอบสนองของระบบจะไม่สามารถลู่เข้าหา 1 โดยทันที เพราะมีเทอมติดลบคอยหักล้างกันในสมการ ซึ่งก็สอดคล้องกับความเป็นจริงเพราะในระบบที่มีค่า damping มาก จะหมายถึงระบบมีการชุดรั้งสูง การที่อินพุตจะทำการบังคับให้ผลตอบสนองมีค่าลู่เข้าสู่ Set point ย่อมต้องการกำลังที่มากตามไปด้วย
เพื่อพิสูจน์ทฤษฎี เราจะนำสมการ (25) ทำการจำลองในโปรแกรม Matlab โดยให้
\(G(s)=\frac{10}{s^{2}+12.6s+10}\)
และมี Matlab script ดังนี้
num4= [10];
den4= [1 12.6 10];
figure (4);
step (num4, den4, t)
stepinfo(tf(num4,den4))
title ('Over Damped Second Order System Response for Step Input');
grid on;
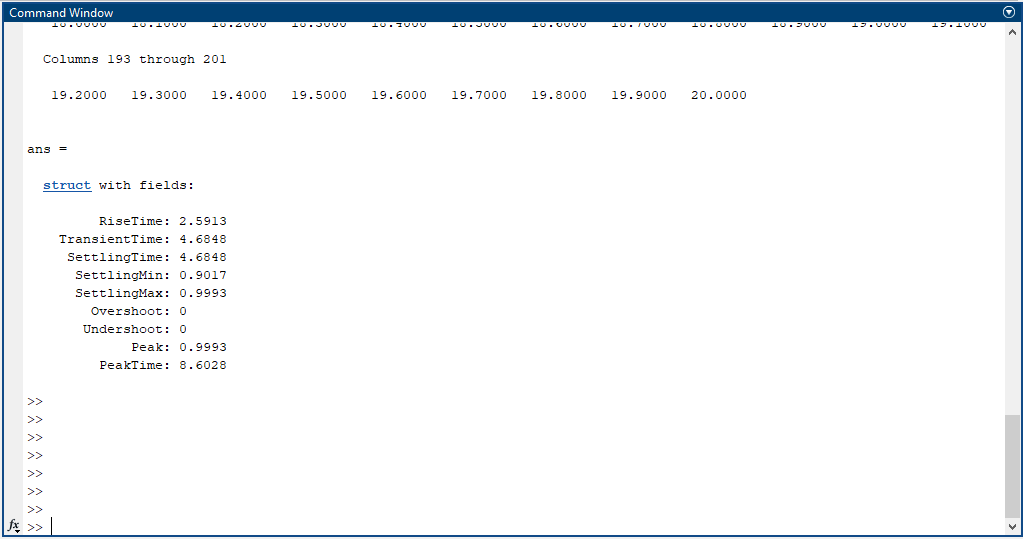
เราสามารถจำลองการทำงานโดยนำ script ข้างต้นไปวางบน Command window ของโปรแกรม Matlab
ท่านที่สนใจสามารถดาวน์โหลด Matlab Script ได้ที่นี้
Post Views: 1,057