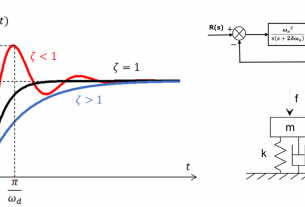
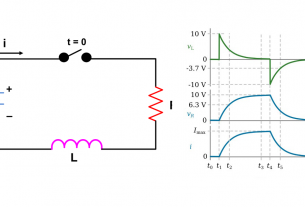
Matlab ได้เตรียมเครื่องมือเอาไว้อย่างมากมายสำหรับงานด้าน Control Systems เราจะเริ่มด้วยการศึกษาพื้นฐานคำสั่งที่จำเป็นสำหรับการออกแบบและวิเคราะห์ระบบควบคุมแบบปิด โดยเริ่มที่คอนโทรลบล๊อกไดอะแกรมดังแสดง
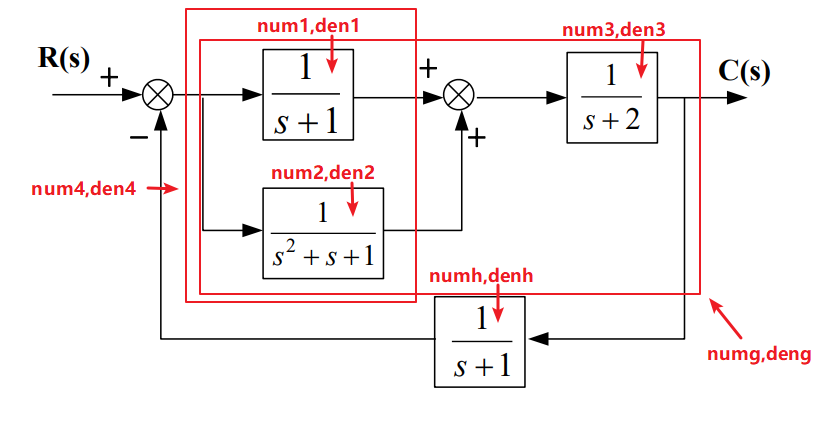
การสร้าง Close Loop Transfer Function ของระบบข้างต้น มีขั้นตอนดังนี้
จะเริ่มจาการสร้าง Transfer Function ย่อย ทั้ง 4 บล๊อก แล้วยุบรวมบล๊อกเข้าด้วยกันตามลำดับ จะได้ Close Loop Transfer Function ในรูปแบบมาตรฐาน โดยมีคำสั่งดังนี้
clc,clear;
num1=[1];
den1=[1 1];
num2=[1];
den2=[1 1 1];
num3=[1];
den3=[1 2];
numh=[1];
denh=[1 1];
[num4,den4]=parallel(num1,den1,num2,den2);
[numg,deng]=series(num4,den4,num3,den3);
[num,den]=feedback(numg,deng,numh,denh,-1);
sys=tf(num,den);
ทำการหาค่ารากของสมการคุณลักณะเฉพาะ และหาค่าโพล และซีโร่ ของระบบ และตรวจสอบว่าระบบมีเสถียรภาพหรือไม่ โดยใช้คำสั่งดังนี้
[z,p,k]=tf2zp(num,den);
s=zpk(z,p,k,-1);
[r,p1,k1]=residue(num,den);
s1=residue(r,p1,k1);
ii=find(real(p)>0);
n1=length(ii);
if(n1>0)
disp(['System is unstable, with ' int2str(n1) 'unstable poles']);
else
disp('Syatem is stable');
end
ทำการแสดง Nyquist Plot โดยคำสั่ง
figure(1)
nyquist(num,den);
grid;
ทำการแสดง Bode Plot โดยคำสั่ง
w=logspace(-2,3,100);
figure(2)
bode(num,den,w);
grid;
ทำการแสดง Root Locus โดยคำสั่ง
figure(3)
rlocus(num,den);
grid;
ทำการแสดงตำแหน่ง Pole-Zero ของระบบ โดยคำสั่ง
figure(4)
pzmap(num,den);
grid;
ทำการทดสอบระบบด้วย อินพุตแบบต่าง โดยคำสั่ง
figure(5)
step(num,den);
figure(6)
impulse(num,den);
figure(7)
t = 0:0.01:10;
u = log(t+1);
lsim(num,den,u,t)
figure(8)
[u,t] = gensig('square',1,10,0.1);
lsim(num,den,u,t)
นอกจากการใช้ Matlab command แล้ว การทดสอบหาผลตอบสนองของระบบต่ออินพุตรูปแบบต่างๆ ยังสามารถใช้ โปรแกรม Simulink ซึ่งจะให้ผลเช่นเดียวกัน
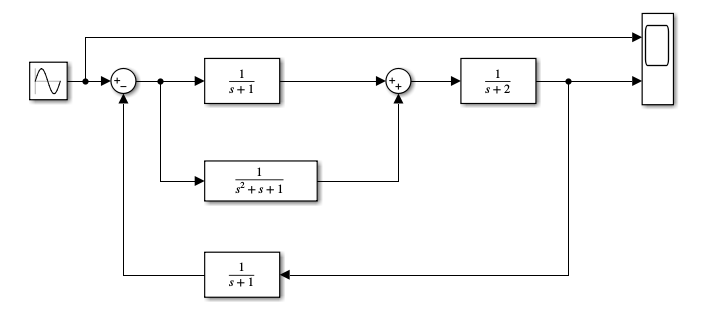
นอกจากตัวอย่างที่ผ่านมาแล้ว หากเรามี Open Loop Transfer Function ดังนี้
(1)
และต้องการเปลี่ยน (1) จะสร้างเป็น Close Loop Transfer Function ดังรูป
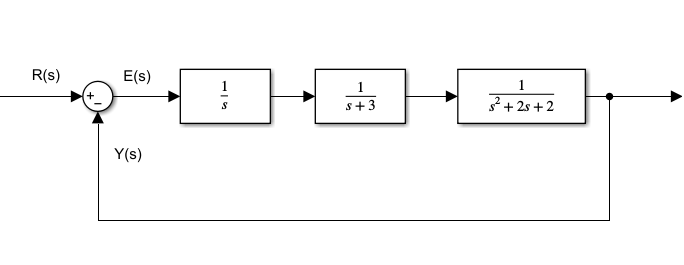
สามารถใช้คำสั่งดังนี้
clc,clear;
num1=[1];
den1=[1 0];
num2=[1];
den2=[1 3];
num3=[1];
den3=[1 2 2];
[num4,den4]=series(num1,den1,num2,den2);
[numg,deng]=series(num3,den3,num4,den4);
[num,den]=cloop(numg,deng,-1);
sys1=tf(num,den)
[z,p,k]=tf2zp(num,den);
sys2=zpk(z,p,k,-1);
[r,p1,k2]=residue(num,den);
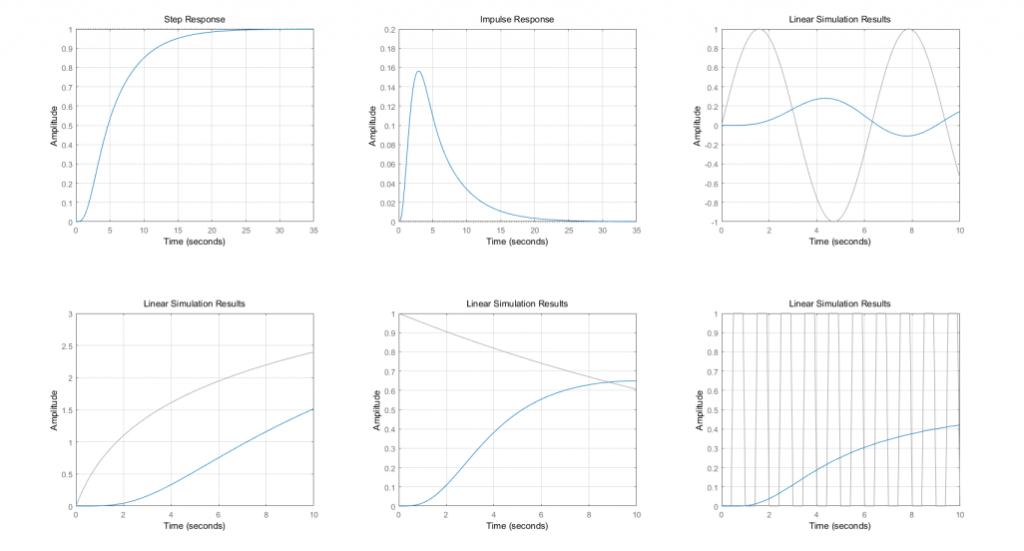
figure(1)
subplot(2,3,1);
step(num,den);
grid
subplot(2,3,2);
impulse(num,den)
grid
subplot(2,3,3);
t = 0:0.01:10;
u = sin(t);
lsim(num,den,u,t)
grid
subplot(2,3,4);
t = 0:0.01:10;
u = log(t+1);
lsim(num,den,u,t)
grid
subplot(2,3,5);
t = 0:0.01:10;
u = exp(-0.05*t);
lsim(num,den,u,t)
grid
subplot(2,3,6);
[u,t] = gensig('square',1,10,0.1);
lsim(num,den,u,t)
grid
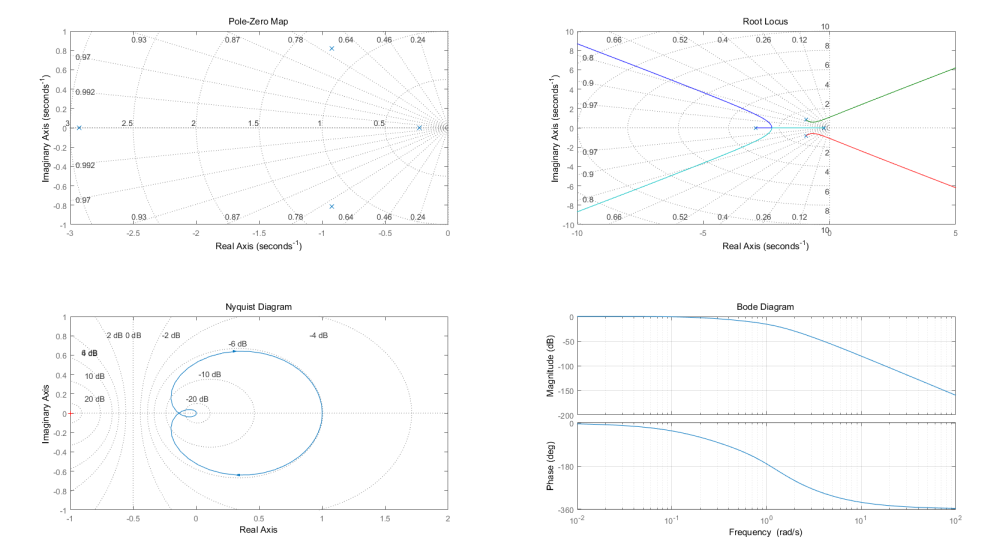
figure(2)
subplot(2,2,1);
pzmap(num,den)
grid
subplot(2,2,2);
rlocus(num,den);
grid
subplot(2,2,3);
nyquist(num,den)
grid
subplot(2,2,4);
bode(num,den)
grid
ii=find(real(p)>0);
n1=length(ii)
if(n1>0)
disp(['System is unstable, with ' int2str(n1) 'unstable poles']);
else
disp('Syatem is stable');
end
สามารถดาวน์โหลด Matlab file ได้ที่นี้