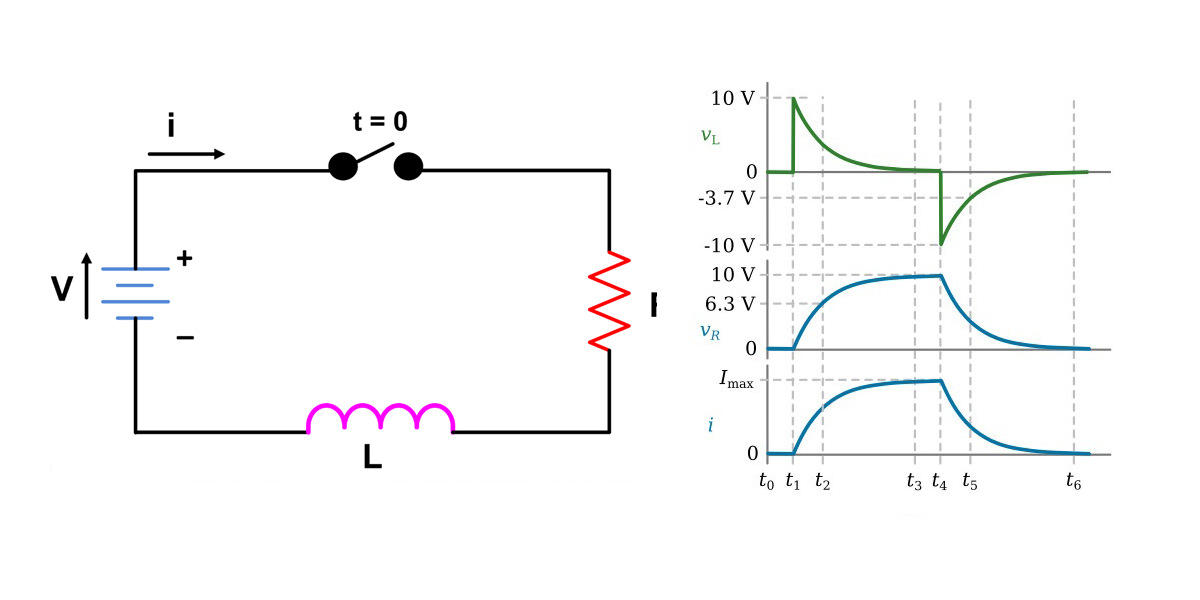
วงจร RL เป็นระบบพลศาสตร์ทางไฟฟ้าที่มีอนุพันธ์อันดับหนึ่ง ในการศึกษาการควบคุมระบบพลศาสตร์ของ วงจร RL เราสามารถเขียน circuit diagram ได้ดังนี้
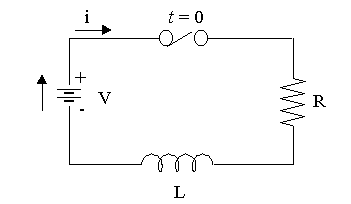
จาก Kirchoff voltage law ทำให้เราได้สมการ
\(L\frac{di}{dt}=u-iR\)
(1)
สมการ (1) เป็นสมการอนุพันธ์อันดับหนึ่ง เมื่อทำการหาผลเฉลยจะได้
\(i=\frac{u}{R}\left ( 1-e^{-(R/L)t} \right )\)
(2)
แต่ทั้งนี้เราจะใช้โปรแกรม Simulink ในการหาผลตอบสนองของระบบ จัดรูปสมการ (1) อีกครั้งจะได้
\(\frac{di}{dt}=\frac{u-iR}{L}\)
(3)
โดยนำสมการ (3) เขียนเป็น Control block diagram โดยกำหนดให้ L=0.01H , R=0.01 Ohm และให้ อินพุต u=400VDC

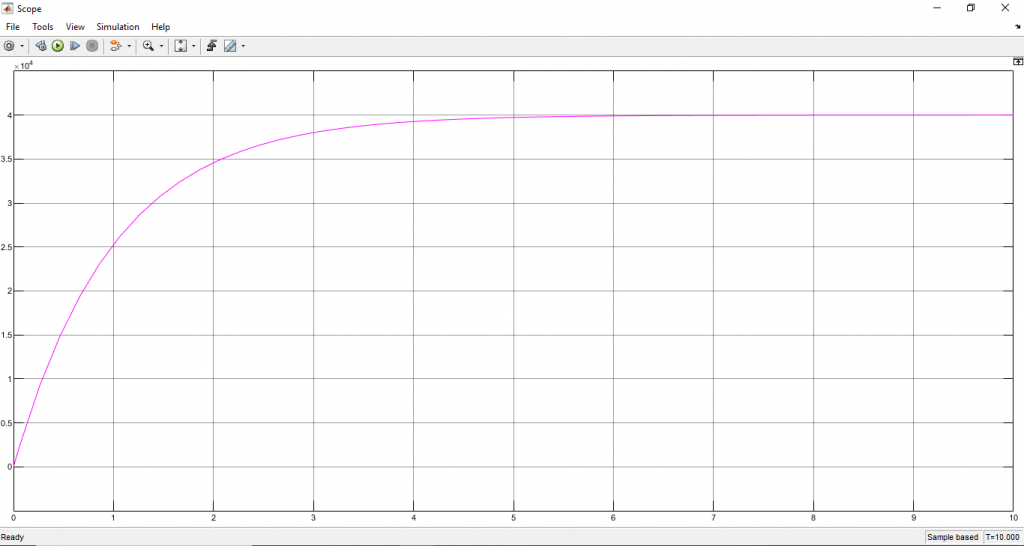
ดาวน์โหลด Matlab/Simulink file ได้ที่นี่