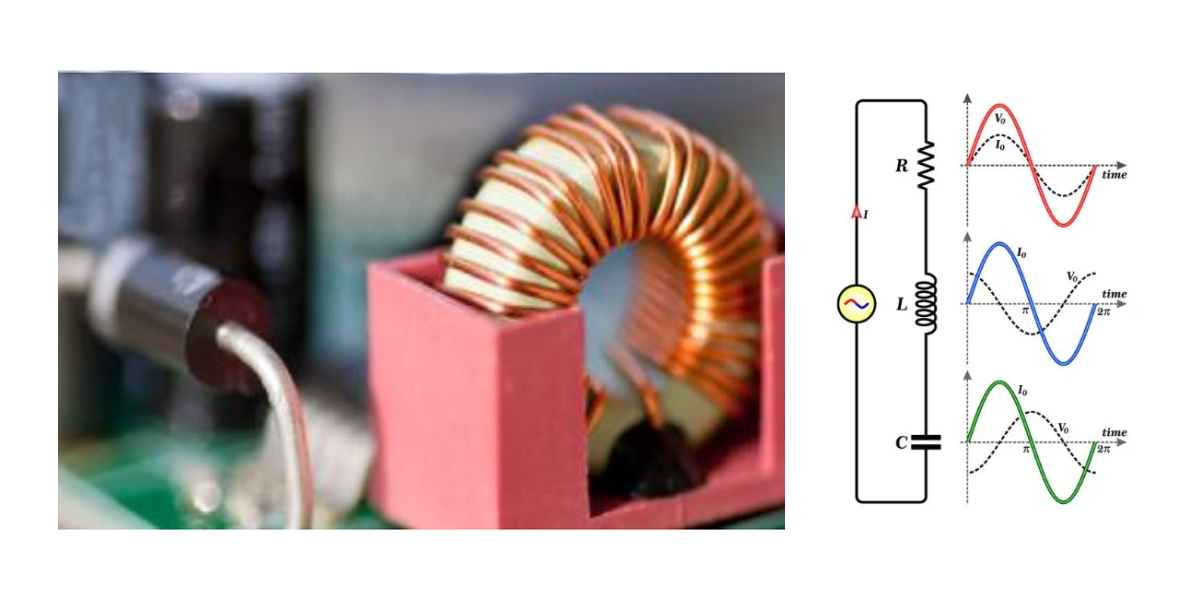
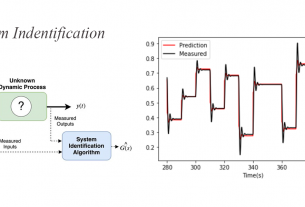
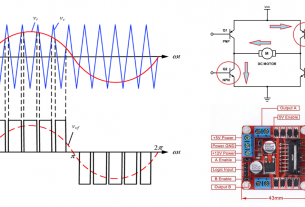
วงจร RLC อนุกรม สามารถเขียน circuit diagram ได้ดังนี้
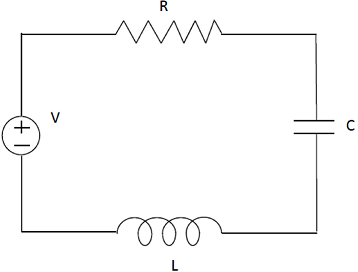
เราจะสร้างแบบจำลองทางพลศาสตร์ของวงจรโดยกำหนดให้
V ค่าแรงดันไฟฟ้าอินพุต
R ค่าความต้านทาน
C ค่าสัมประสิทธิประจุกระแสไฟฟ้า
L ค่าความเหนี่ยวนำ
จาก Kirchhoff voltage law จะได้
\(v_{R}+v_{L}+v_{C}=v_{in}\)
(1)
จากทฤษฎีวงจรไฟฟ้า เราทราบว่าแรงดันตกคล่อมความต้าน คือ
\(v_{R}=Ri_{R}\)
(2)
แรงดันตกคล่อมขดลวดเหนียวนำ คือ
\(v_{L}=L\frac{di_{L}}{dt}\)
(3)
กระแสไฟฟ้าผ่านตัวเก็บประจุ คือ
\(i_{c}=C\frac{dv_{c}}{dt}\)
(4)
จากไดอะแกรม กระแสไฟฟ้าในวงจรอนุกรม จะเป็น
\(i_{R}=i_{L}=i_{C}\)
(5)
จาก สมการ (1) , (2) , (3) , (4) และ (5) เราสามารถเขียนสมการอนุพันธ์ของวงจร RLC ได้ดังนี้
\(LC\frac{d^{2}v_{c}}{dt^{2}}+RC\frac{dv_{c}}{dt}+v_{c}=v_{in}\)
(6)
จัดรูปสมการ (6) จะได้
\(\frac{d^{2}v_{C}}{dt^{2}}=-\frac{R}{L}\frac{dv_{C}}{dt}-\frac{1}{LC}v_{c}+\frac{1}{LC}v_{in}\)
\(\frac{d^{2}v_{C}}{dt^{2}}=\frac{1}{LC}\left( -RC\frac{dv_{c}}{dt}-v_{c}+v_{in} \right)\)
(7)
เราจะใช้สมการ (7) ในการพัฒนาแบบจำลองทางพลศาสตร์ของวงจร RLC หรือสามารถเปิดจากไฟล์แนบของบทความชิ้นนนี้จะได้
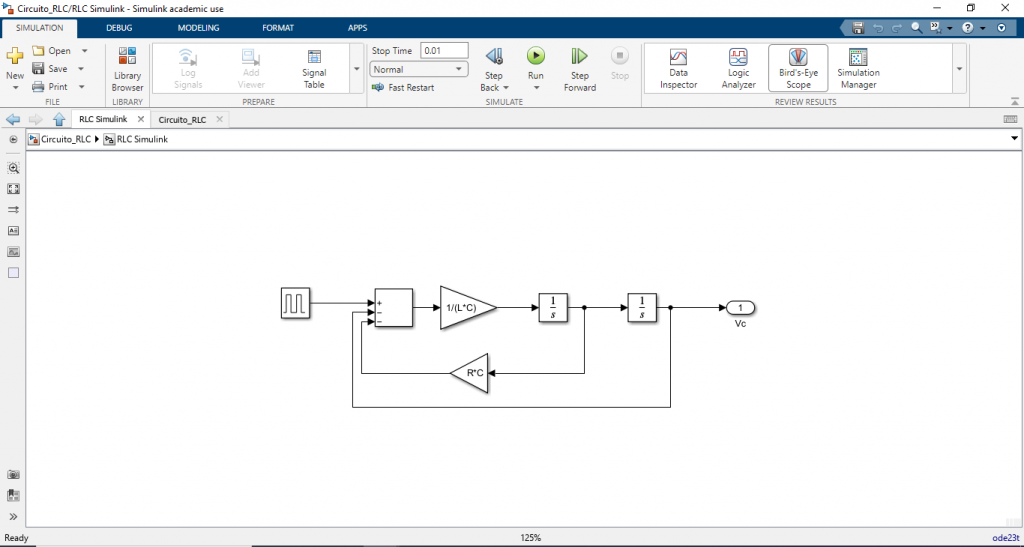
กำหนดค่าพารามิเตอร์ของวงจรลงใน Parameter_RLC.m แล้วทำการ RUN ดังนี้
%Parameters
C=0.1e-6;
R=100;
L=4e-3;
Vin=5;
open RLC_circuit.slx
sim("RLC_circuit.slx")
จะได้ผลลัพธ์จากการทำ Simulation ดังนี้
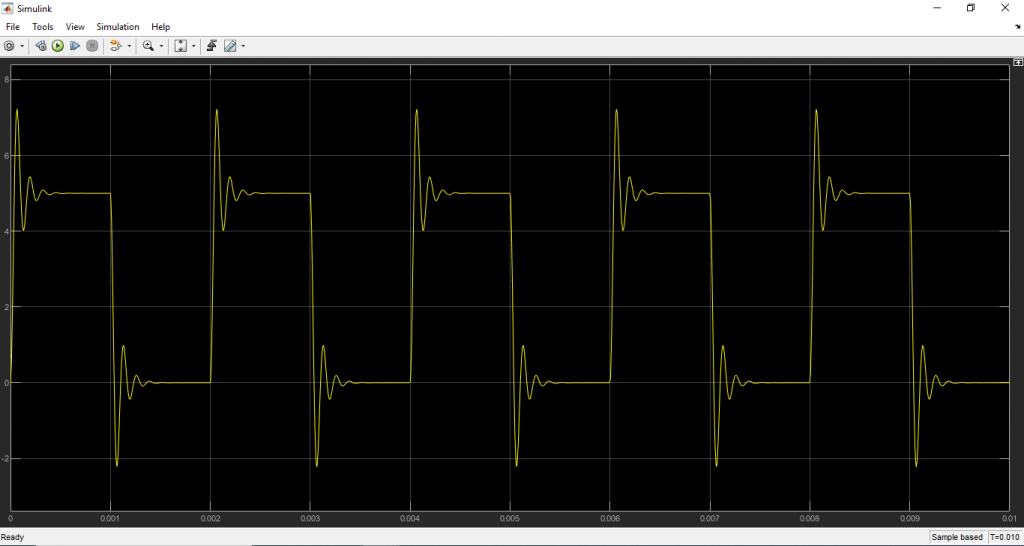
ดาวน์โหลดไฟล์ Simulink ได้ที่นี่