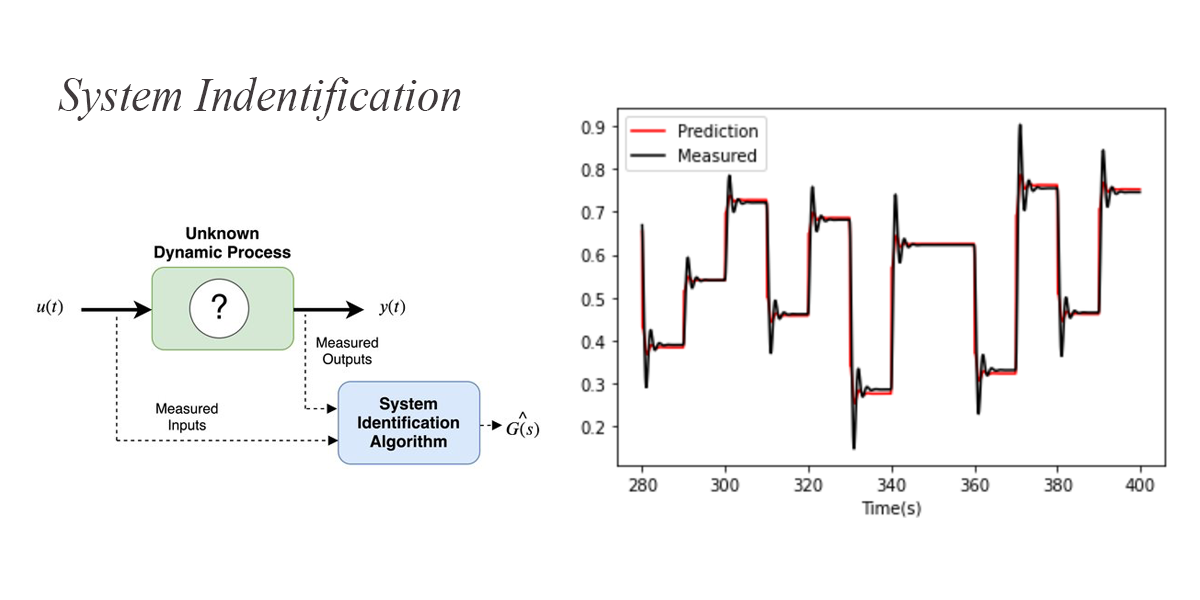
ในกรณีที่เราไม่ทราบสมการพลศาสตร์ของระบบ แต่เราสามารถทดสอบระบบโดยการป้อนอินพุตแบบ Unit Step และทำการบันทึกผลตอบสนอง เราก็สามารถใช้ Transfer function ของระบบพลศาสตร์ที่มีอนพันธ์อันดับสองในการประมาณ Transfer function ของระบบที่เราสนใจได้
ระบบที่เราจะประมาณการ ควรให้ผลตอบสนองออกมาในแนวโน้มเดียวกับระบบพลศาสตร์ที่มีอนุพันธ์อันดับสอง
ระบบพลศาสตร์ที่มีอนุพันธ์อันดับสอง สามารถเขียนในรูปทั่วไปได้ดังนี้
(1)
\(\delta\) คือ dampling ratio
\(\omega_{n}\) คือความถี่ธรรมชาติของระบบ (Natural frequency)
ตัวอย่างการคำนวณ จะขอยกมาจากหนังสือของ Nise ดังภาพนี้
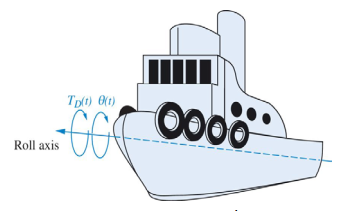
มีเรือล่องไปในแม่น้ำที่สงบ แล้วเกินคลื่นขึ้นมาหนึ่งลูกวิ่งเข้าปะทะกับตัวเรือ ทำให้หน้าเรือมีการหมุนรอบแกน Roll โดยเราจะสมมติให้เคลื่อนที่เข้ามาปะทะมีลักษณะเป็น Unit step และ มุมของหัวเรือที่มีการมุมรอบแกน Roll คือผลตอบของระบบ
กับตันได้ตรวจสอบระบบบันทึกค่ามุม Roll ของหัวเรือในช่วงขณะเวลาหนึ่งพบว่าเป็นดังนี้
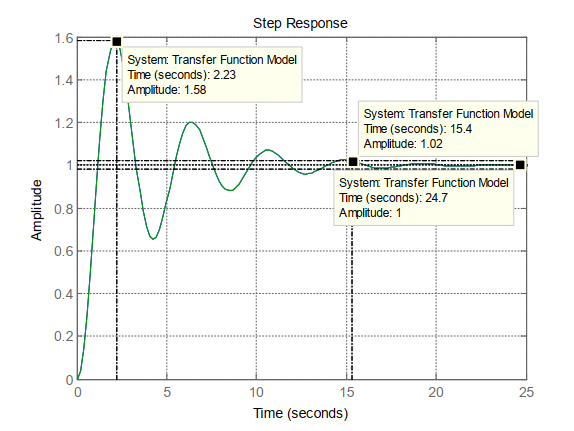
จากบันทึกของกับตันเรือเราพบว่า มุมของหัวเรือรอบแกน Roll มีลักษณะที่จะใช้ Transfer function ของระบบพลศาสตร์ที่มีอนุพันธ์อันดับสองประมาณค่าได้ ดังนี้
คำนวณหา เปอเซนต์ % Over shoot ได้โดยสมการ
(2)
Dampling ratio คำนวณได้จากสมการ
(3)
Settling Time \(T_{s}\) จะประมาณการจากรูปที่ 1. เมื่อเวลาผลตอบสนองของระบบ อยู่ในระดับ \(\pm 2%\)
ความถี่ธรรมชาติของระบบคำนวณได้จากสมการ
(4)
ค่า Time constant หาได้จาก
(5)
ค่า Settling time นอกจากจะประมาณจากผลตอบสนองของระบบดังปรากฎในรูปที่ 1 แล้ว ยังพบว่าระบบพลศาสตร์อนุพันธ์อันดับสอง จะลู่เข้าหา 98% ของค่าสุดท้าย (Final value) ที่ประมาณ 4 เท่าของค่า Time Contstant เขียนเป็นสมการได้ดังนี้
(6)
จากรูปที่ 1 และ สมการ (2) จะได้ %Over Shoot = 58%
จากสมการ (3) จะได้ค่า \(\delta\) = 0.1708
จากรูปที่ 1 จะได้ค่า \(T_{s}\)= 15.4 Sec.
จากสมการ (4) จะได้ค่า \( \omega_{n} \)= 1.4925 rad/s
นำพารามิเตอร์ที่ได้จากการประมาณการ ไปทดสอบในโปรแกรม Matlab โดย Script ดังนี้
clc
clear
% Declaration of Omega_n Value
wn = 1.4925; %***** Our system **** %
% Zeta Values for Each Variation
z1 = 1;
z2 = 2;
z3 = 0.1708; %***** Our system **** %
z4 = 0.5;
z5 = 0;
% Numerator and Denominator Values for Each Variation
num1 = wn^2;
den1 = [1 2*z1*wn wn^2];
num2 = wn^2;
den2 = [1 2*z2*wn wn^2];
num3 = wn^2;
den3 = [1 2*z3*wn wn^2];
num4 = wn^2;
den4 = [1 2*z4*wn wn^2];
num5 = wn^2;
den5 = [1 2*z5*wn wn^2];
figure;
% When Zeta = 1
sys_tf1 = tf(num1, den1);
% Pole Zero Map
subplot(2,5,1)
pzmap(sys_tf1);
title(['Pole Zero Map (Zeta = ', num2str(z1), ')'])
% Step Response
subplot(2,5,6)
step(sys_tf1);
title(['Step Response (Zeta = ', num2str(z1), ')'])
% When Zeta = 2
sys_tf2 = tf(num2, den2);
% Pole Zero Map
subplot(2,5,2)
pzmap(sys_tf2);
title(['Pole Zero Map (Zeta = ', num2str(z2), ')'])
% Step Response
subplot(2,5,7)
step(sys_tf2);
title(['Step Response (Zeta = ', num2str(z2), ')'])
% When Zeta = 0.1
sys_tf3 = tf(num3, den3);
% Pole Zero Map
subplot(2,5,3)
pzmap(sys_tf3);
title(['Pole Zero Map (Zeta = ', num2str(z3), ')'])
% Step Response
subplot(2,5,8)
step(sys_tf3);
title(['Step Response (Zeta = ', num2str(z3), ')'])
% When Zeta = 0.5
sys_tf4 = tf(num4, den4);
% Pole Zero Map
subplot(2,5,4)
pzmap(sys_tf4);
title(['Pole Zero Map (Zeta = ', num2str(z4), ')'])
% Step Response
subplot(2,5,9)
step(sys_tf4);
title(['Step Response (Zeta = ', num2str(z4), ')'])
% When Zeta = 0
sys_tf5 = tf(num5, den5);
% Pole Zero Map
subplot(2,5,5)
pzmap(sys_tf5);
title(['Pole Zero Map (Zeta = ', num2str(z5), ')'])
% Step Response
subplot(2,5,10)
step(sys_tf5,5);
title(['Step Response (Zeta = ', num2str(z5), ')'])
% Displaying damping mode information and time domain specifications
for z = [z1, z2, z3, z4, z5]
if z == 0
disp(['Mode of damping for Zeta = ', num2str(z), ': Undamped']);
elseif 0 < z && z < 1
% Displaying damping mode information
disp(['Mode of damping for Zeta = ', num2str(z), ': Underdamped']);
% Calculating and displaying time domain specifications
% Rise Time
tr = pi / (wn * sqrt(1 - z^2));
disp(['Rise Time: ', num2str(tr)]);
% Settling Time
ts = 4 / (z * wn);
disp(['Settling Time: ', num2str(ts)]);
% Natural Frequency of Oscillation
fn = wn * sqrt(1 - z^2);
disp(['Natural Frequency of Oscillation: ', num2str(fn)]);
elseif z == 1
disp(['Mode of damping for Zeta = ', num2str(z), ': Critically Damped']);
elseif z > 1
disp(['Mode of damping for Zeta = ', num2str(z), ': Overdamped']);
end
disp(' '); % Empty line break
end
figure(2);
bode(sys_tf1,sys_tf2,sys_tf3,sys_tf4,sys_tf5)
title('Bode Plot')
grid on;
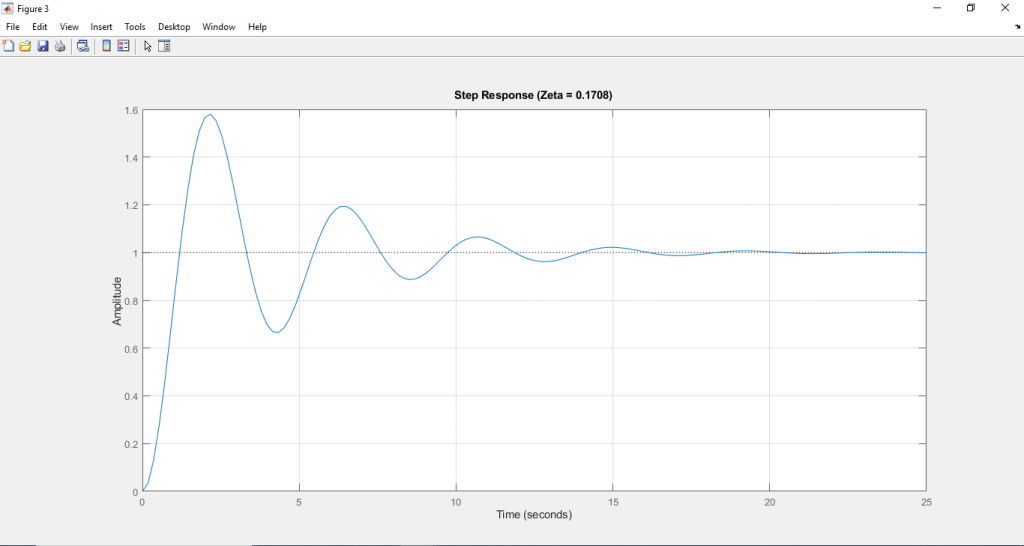
figure(3)
step(sys_tf3);
title(['Step Response (Zeta = ', num2str(z3), ')'])
grid on;
จะได้ผลลัพธ์ดังนี้

ดาวน์โหลด Matlab Script ได้ที่นี่