Ziegler-Nichols วิธีที่ 1 ปรับแต่ง PID Controller โดยไม่ต้องทราบ สมการพลศาสตร์ของระบบ -

เพื่อให้ผลตอบสนองของระบบเป็นไปตามต้องการ การใช้ตัวควบคุมเช่น ตัวควบคุมแบบพีไอดี (PID Controller) เป็นทางเลือกที่ได้รับความนิยม คาดว่าตัวควบคุมในอุตสาหกรรม 90% จะเป็นตัวควบคุมแบบพีไอดี โดยปกติแล้วการปรับตั้งค่าพารามิเตอร์ของ PID นั้นจำเป็นจะต้องทราบ Close loop dynamical system ของระบบ ซึ่งไม่ค่อยสะดวกสำหรับผู้ปฏิบัติงาน

บ่อยครั้งเป็นเรื่องที่ยากที่จะหาแบบจำลองทางพลศาสตร์ของระบบ การปรับแต่งตัวควบคุมกรณีนี้สามารถทำได้โดยใช้วิธีแนะนำของ Ziegler-Nichols Method

Ziegler-Nichols Method มีให้เลือกใช้ 2 วิธี คือ The first method และ The second method ในงานชิ้นนี้จะนำเสนอการปรับแต่งตัวคุมคุม โดยใช้ The first method ทั้งนี้ก็เพราะวิธีการนี้ไม่จำเป็นต้องเพิ่มขนาดอินพุตไปเรื่อยๆ จนระบบเกิดการ Oscillation ซึ่งในบางกระบวนการ การเพิ่มขนาดอินพุตจนระบบเกิด Oscillation มีความอันตราย หรือต้องใช้อินพุตขนาดใหญ่ แต่วิธีการ The first method เราจะใช้ผลตอบสนองของระบบแบบเปิดมาทำการคำนวณค่าพารามิเตอร์ของพีไอดีแบบวงปิด

ระบบควบคุมกระบวนการแบบวงปิด(Close loop system) โดยใช้ตัวควบุคมแบบพีไอดี สามารถแสดงได้ดังรูป

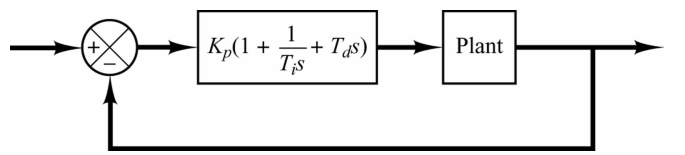
จากบล๊อกไดอะแกรมด้านบน(หรือระบบจริงหน้างาน) เราไม่ทราบว่ากระบวนการที่เราจะควบคุม (Plant) มีสมการพลศาสตร์เป็นอย่างไร จึงไม่สามารถใช้เครื่องมือเช่น Root Locus, Bode หรือ Nyquist เพื่อช่วยออกแบบตัวควบคุมได้

เราจะเริ่มวิธีการ Ziegler-Nicoles the first method ด้วยการปิดสัญญาณป้อนกลับและนำตัวควบคุมออกไปก่อน ให้ระบบกลายเป็นระบบควบคุมแบบเปิด ดังแสดงในภาพด้านล่าง

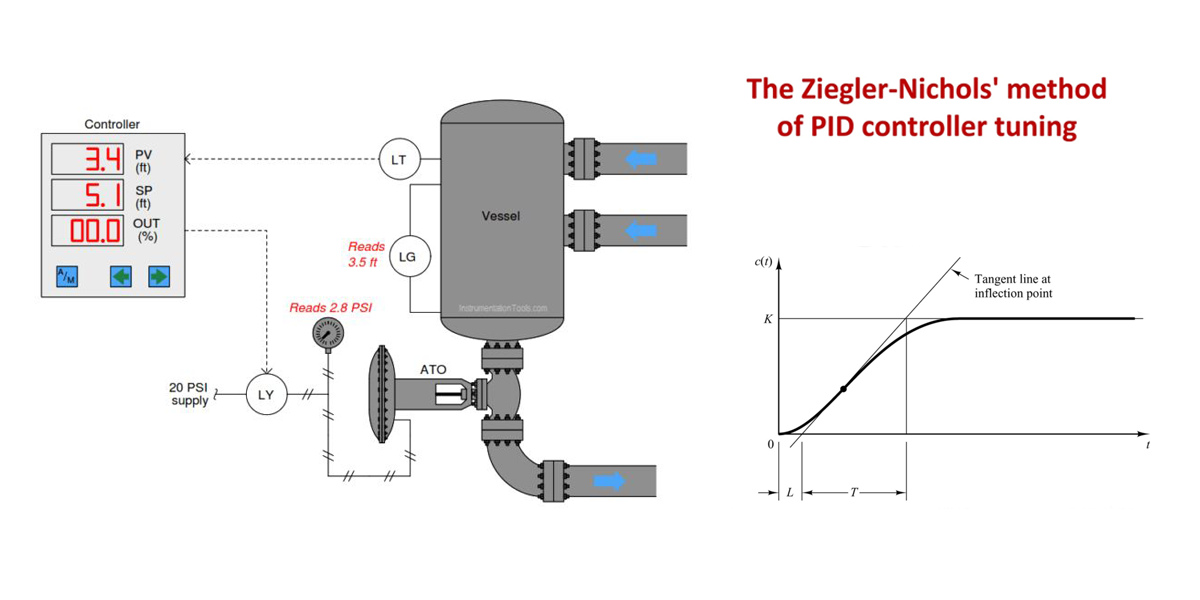
หลังจากได้ระบบแบบเปิดแล้วให้ทำการป้อนอินพุตที่เหมาะสมค่าหนึ่งที่ทำระบบแบบเปิดให้ผลตอบสนองประมาณ 60-90% ของผลอินพุต แล้วบันทึกค่าผลตอบสนองดังแสดงในภาพด้านล่าง เราจะเรียกว่า Reaction curve

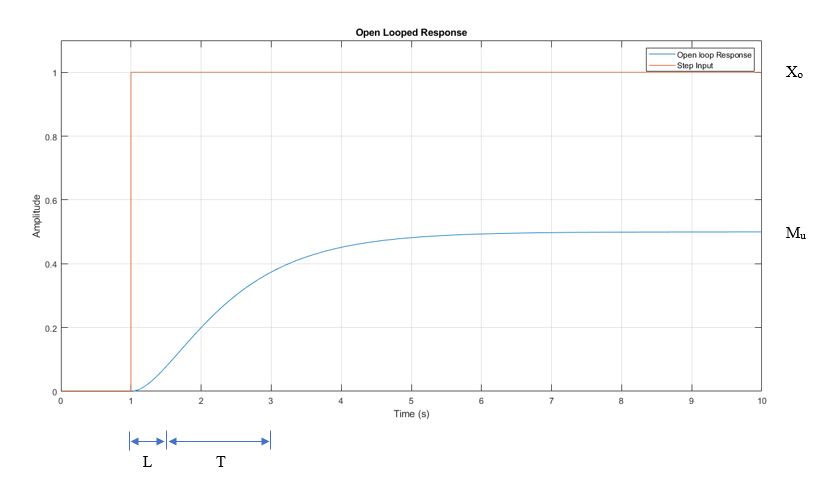
จากภาพจะเป็นการป้อนอินพุตเป็น Unit step ขนาด 1 (100% norminal rated) แล้วทำการบันทึกค่าผลตอบสนอง ปรากฎว่าระบบให้ผลตอบสนองออกมา 0.5( 50% norminal rated )จากการอ่านบันทึกการทดลอง จะพบว่า

Xo คือค่าอินพุตที่ป้อนให้กับระบบ = 1

Mu คือค่าผลตอบสนองของระบบแบบเปิด = 0.5

L คือช่วงเวลา dead zone ก่อนที่ผลตอบสนองของระบบจะเพิ่มขึ้นถึง 10% = 0.5 Sec.

T คือช่วงเวลาจาก 10% – 100% ของผลตอบสนอง = 1.5 Sec.

พิจารณาสมการ PID Controller จะได้

\(\frac{U(s)}{E(s)}=K_{p}\left (1+\frac{1}{T_{I}s}+T_{D}s \right )\)

(1)

Ziegler-Nichols ‘s the first method ได้แนะนำการคำพารามิเตอร์ของพีไอดีไว้ดังนี้

\(K_{o}=\frac{X_{o}T}{M_{u}L}\)

(2)

หรือในบางตำราจะแนะนำให้เริ่มต้นคำนวณ Ko ดังนี้

\(K_{o}=\frac{T}{L}\)

(3)

พบว่าส่วนใหญ่แล้วนิยมใช้สมการ (3) เป็นตัวตั้งต้นในการคำนวณค่าพารามิเตอร์ของ PID Controller เมื่อได้ Ko แล้ว วิธีการ The first method ได้ให้คำแนะนำในการคำนวณค่าอื่นๆ ไว้ดังนี้

\(K_{p}=1.2K_{o}\)

(4)

\(T_{I}=2L\)

(5)

\(T_{D}=0.5L\)

(6)

\(K_{i}=\frac{K_{p}}{T_{I}}\)

(7)

\(K_{d}=\frac{K_{p}}{T_{D}}\)

(8)

ค่าที่ได้จากสมการ (4) , (7) และ (8) จะถูกนำไปใช้เป็นพารามิเตอร์ของ PID Controller เพื่อควบคุมกระบวนการแบบวงปิด(Close loop)

เราจะทำการทดสอบ Ziegler-Nicoles ‘s the first method โดยใช้โปรแกรม Simulink โดยสมมติว่าเรามีระบบควบคุมแบบปิดที่ไม่ทราบ Transfer function ของระบบ จึงทำการปลดระบบจากระบบควบคุมปิดให้เป็นระบบเปิด ทำการป้อนอินพุตให้กับระบบ และบันทึกค่าเพื่อให้ได้ Reaction Curve แล้วทำการคำนวณพีไอดีพารามิเตอร์ตามสมการ (3) – (8) เราจะได้ Kp , Ki และ Kd ที่จะถูกนำไปใช้สำหรับระบบควบคุมแบบวงปิดต่อไป

ทำการเปิดไฟล์ Simulink จะพบว่าเราได้ทำการปลดระบบป้อนกลับออก จนระบบกลายเป็นควบคุมแบบเปิด

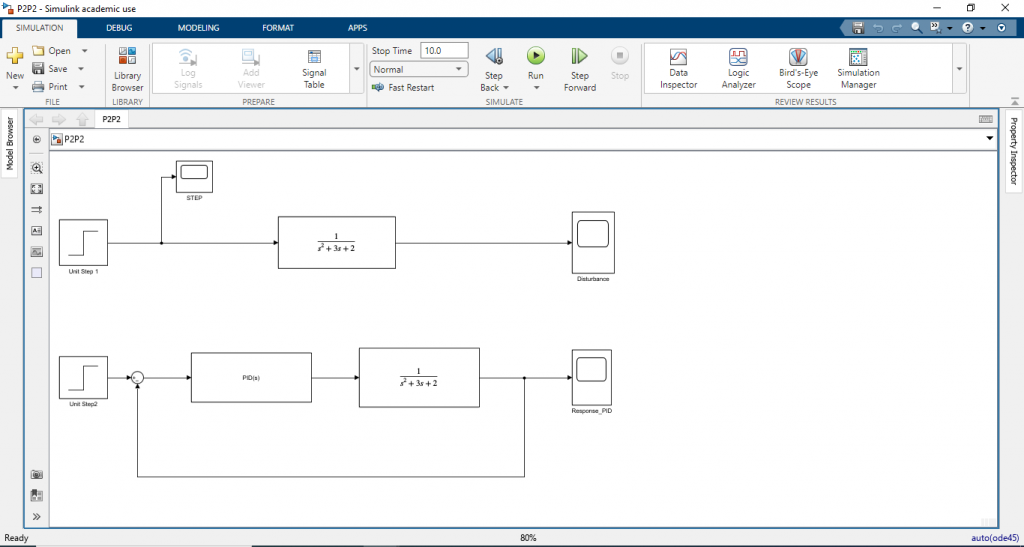
และทำการเปิดไฟล์ Main_script.m และทำการ RUN

clear; clc; close all; % Clears the workspace and command window.

t0 = 0;
ti = 0.01;
tf = 10;
dt = 1E-2;

L = 0.5;   % Time dead Zone
T = 1.5;   % Time from 10% - 80%

%Kp = 1.2*(1/0.5)*(T/L);  % Recommendation from Text book
Kp = 1.2*(T/L);           % From my experience

Ti = 2*L;
Td = 0.5*L;

Ki = Kp/Ti;
Kd = Kp*Td;

%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Call Simulink Block Diagram%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
open_system('P2P2.slx')
ansRAMP = sim('P2P2.slx');

%%
%%%%%%%%%%%%%%%%%%%%%
%Plot Control System%
%%%%%%%%%%%%%%%%%%%%%
hold all % This is so each plot is actually gets plotted instead of overriding each other. 

figure (1);
plot(ansRAMP.Disturbance(:,1),ansRAMP.Disturbance(:,2));
hold on;
plot(ansRAMP.Response_PID(:,1),ansRAMP.Response_PID(:,2));
hold on;
plot(ansRAMP.STEP(:,1),ansRAMP.STEP(:,2));
title('PID Controller Design');
xlabel('Time (s)');
ylabel('Amplitude');
legend('Open loop Response', 'PID Response', 'Step Function');
grid on;

hold on;
figure (2); 
plot(ansRAMP.Disturbance(:,1),ansRAMP.Disturbance(:,2));
hold on;
plot(ansRAMP.STEP(:,1),ansRAMP.STEP(:,2));
title('Open Looped Response');
xlabel('Time (s)');
ylabel('Amplitude');
legend('Open loop Response', 'Step Input');
grid on;

เราจะได้ผลตอบสนองของระบบแบบเปิด ให้ทำการหาค่า L และ T เพื่อนำไปใช้ในการคำนวณหาค่าพารามิเตอร์ของตัวควบคุมแบบพีไอดีต่อไป

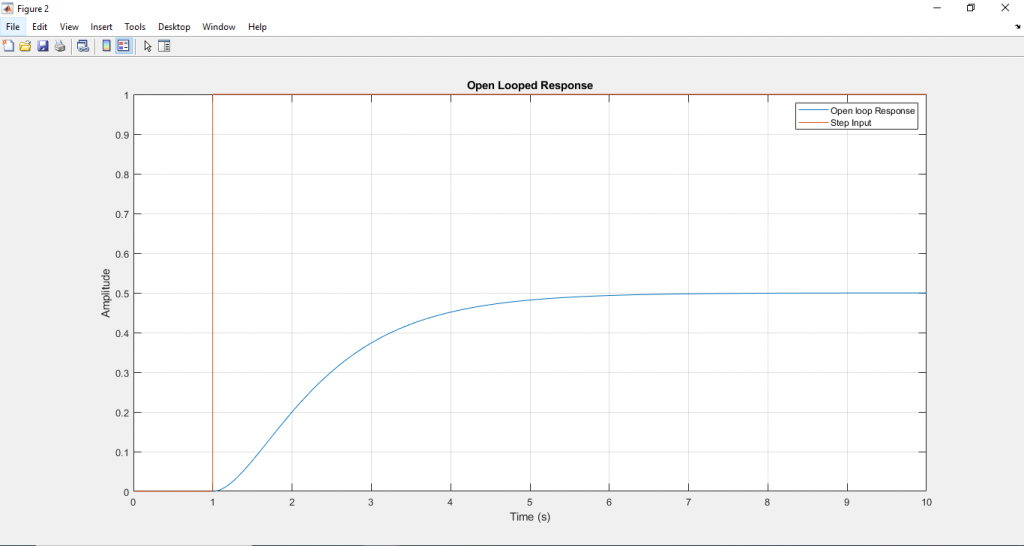
หลังจากนั้นให้นำค่าพารามิเตอร์ของพีไอดีคอนโทรลเลอร์ที่คำนวณได้ กำหนดลงไปในตัวควบคุมแบบพีไอดี ภายในสคริป Main_script.m เพื่อทำการจำลองการทำงานของระบบแบบวงปิด เราจะได้ผลตอบสนองแบบปิดดังนี้

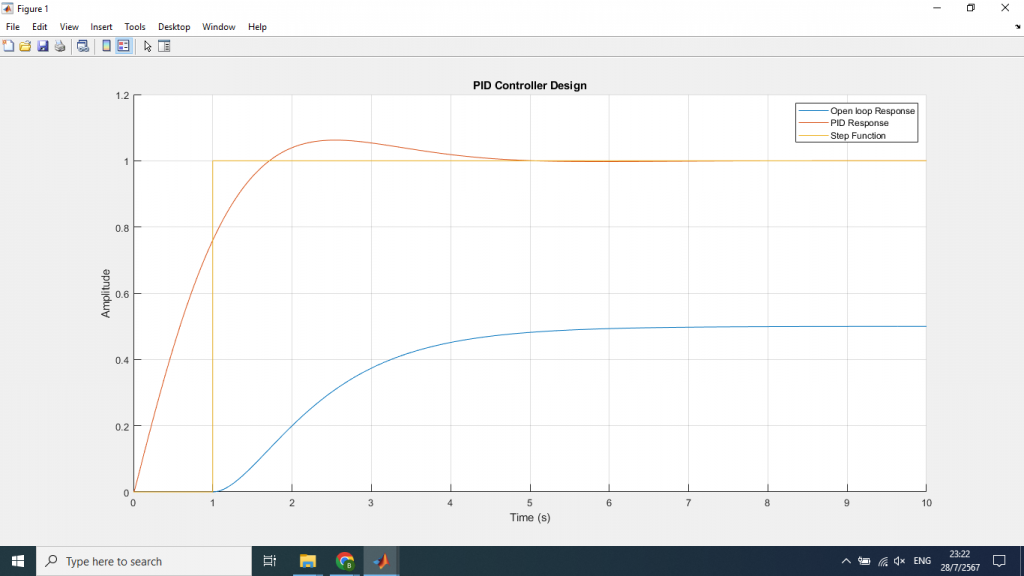
จากตัวอย่างเราจะได้ค่าพารามิเตอร์ของ PID Controller โดยไม่จำเป็นต้องทราบแบบจำลองทางพลศาสตร์ของกระบวนการเลย จากการ Simulation พบว่า PID Controller สามารถควบคุมกระบวนการให้ผลตอบสนอนลู่เข้าหา Set point ตามต้องการภายในเวลา 5 วินาที

ดาวน์โหลด Simulink file ได้ที่นี่