บล๊อกก่อนหน้านี้เราได้ศึกษาการหาค่าพารามิเตอร์ของ PID โดยตั้งระบบให้กลายเป็น Open Loop ก่อน Ziegler-Nichols วิธีปรับแต่ง PID Controller โดยไม่ต้องทราบ สมการพลศาสตร์ของระบบ ในบล๊อกนี้เราจะศึกษา Ziegler-Nicoles Method 2 ซึ่งจะสามารถหาค่าพารามิเตอร์ PID โดยไม่จำเป็นต้องทราบสมการพลศาสตร์ของระบบ ในขณะที่ระบบยังมีการทำงานแบบวงปิด(Close Loop)
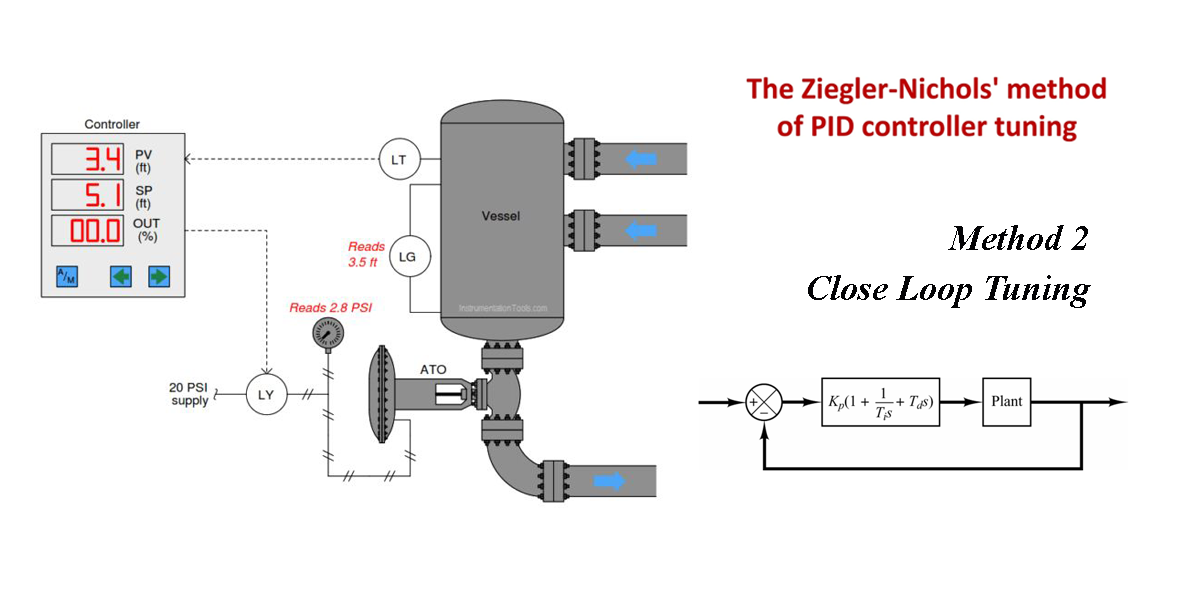
โดยปกติแล้วระบบป้อนกลับ (Feedback control) ที่มีตัวควบคุม PID จะแสดงได้ดังรูปที่ 1
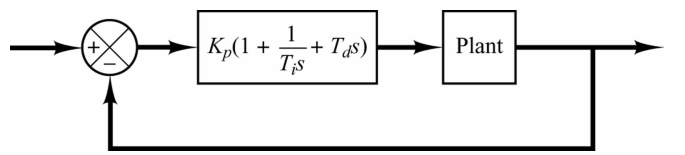
ให้เราดำเนินการปิดตัวควบคุม I และ D ออกไปก่อนให้เหลือเฉพาะตัวควบคุม P แสดงดังรูปที่ 2
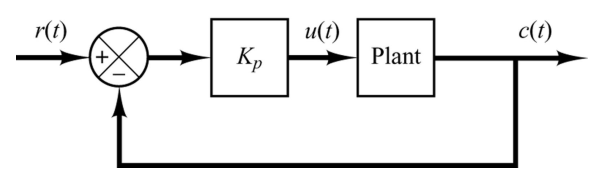
จากบล๊อก การหาทางเดินของราก(Root Locus) ของระบบพลศาสตร์ โดยโปรแกรม Matlab เราทราบว่าการเพิ่มค่า Kp มากขึ้นเรื่อยๆ มีผลต่อสมการคุณลักษณะเฉพาะของระบบ ทำให้ค่า poles ของระบบเปลี่ยนแปลงไป การเพิ่มอัตราขยายจนระบบเกิดการ Oscillation ก็คือการย้ายโพลของระบบให้เหลือเฉพาะโพลที่อยู่บนแกนจินตภาพ Ziegler-Nicoles the First method จะเรียนค่าอัตราขยายนี้ว่า Kcr และ คาบเวลาของการเกิด Oscillation ว่า Pcr ดังแสดงในรูปที่ 3

เราจะทำการค่อยเพิ่มค่า Kp ให้มากขึ้นเรื่อยๆ จนระบบเกิดการ Oscillation อย่างไรก็ตามการใช้วิธีนี้ต้องกระทำด้วยความระมัดระวัง การเพิ่มอัตราขยายจนระบบเกิดการ Oscillation ในบางระบบอาจจะก่อให้เกิดความเสียหายแก่อุปกรณ์ทางไฟฟ้าและทางกล ก็เป็นได้ หากมีความเสี่ยงผู้เขียนแนะนำให้ใช้วิธีการ Ziegler-Nicoles the first Method ที่ศึกษาในบล็อก Ziegler-Nichols วิธีปรับแต่ง PID Controller โดยไม่ต้องทราบ สมการพลศาสตร์ของระบบ
เรามาจำลองการทำงานโดยโปรแกรม Matlab ดังนี้
1) เพื่อการจำลองการทำงาน Ziegler Nicols the โirst method เราจะสร้าง Open Loop Transfer function ของระบบหนึ่งที่เรากำลังจะหาพารามิเตอร์พีไอดี ลงบนโปรแกรม Matlab ดังนี้ (แต่ในความเป็นจริงเราไม่ทราบ Transfer function)
%% Plant (open-loop plant)
Gp = tf(523500, [1 87.35 10470 0])
2) ทำให้ Open Loop Transfer function กลายเป็นระบบ close loop ตามรูปที่ 2 และทดสอบระบบด้วยปิดด้วย Step Input ด้วยคำสั่ง
%% Plant (make it close Loop)
Gpp = feedback(Gp, 1)
step(Gpp, 1), grid on
จะได้ผลตอบสนองดังนี้
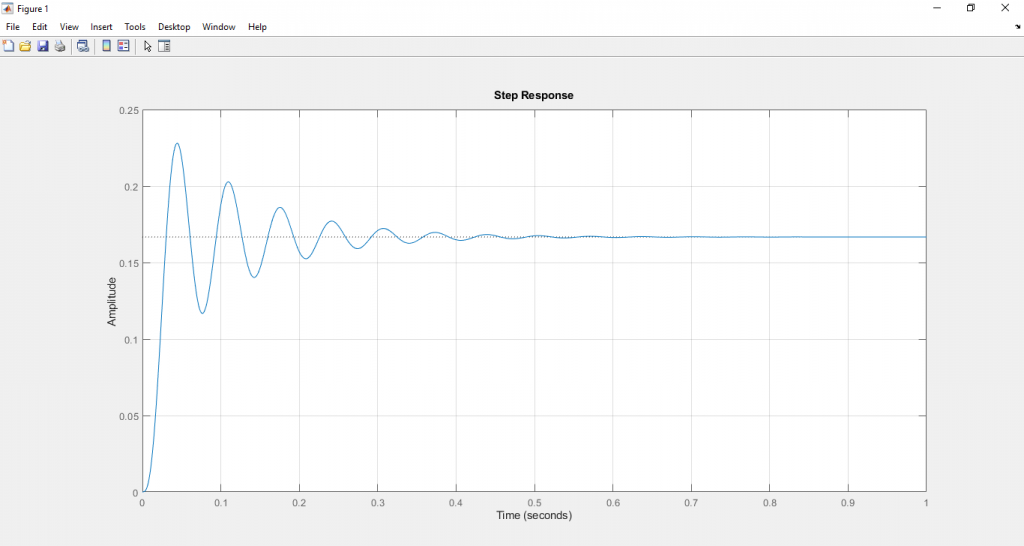
3) ให้ทดลองปรับค่า K ไปเรื่อยๆ จนระบบเกิดการ Oscillation ซึ่งผู้เขียนได้ทดลองปรับตั้งแต่ 0.1 – 0.747 ซึ่งทำให้เราทราบว่า Kcr = 0.747 ด้วยคำสั่ง
%% Ziegler–Nichols Gains Test until Oscilation
Kcr= 0.747; % Find this Ultimate Gain
%K=0.6;
%K=0.5;
%K=0.4;
%K=0.3;
%K=0.2;
%K=0.1;
G= minreal(feedback(Kcr*Gpp, 1));
step(G, 1), grid on
จะได้ผลตอบสนองดังนี้
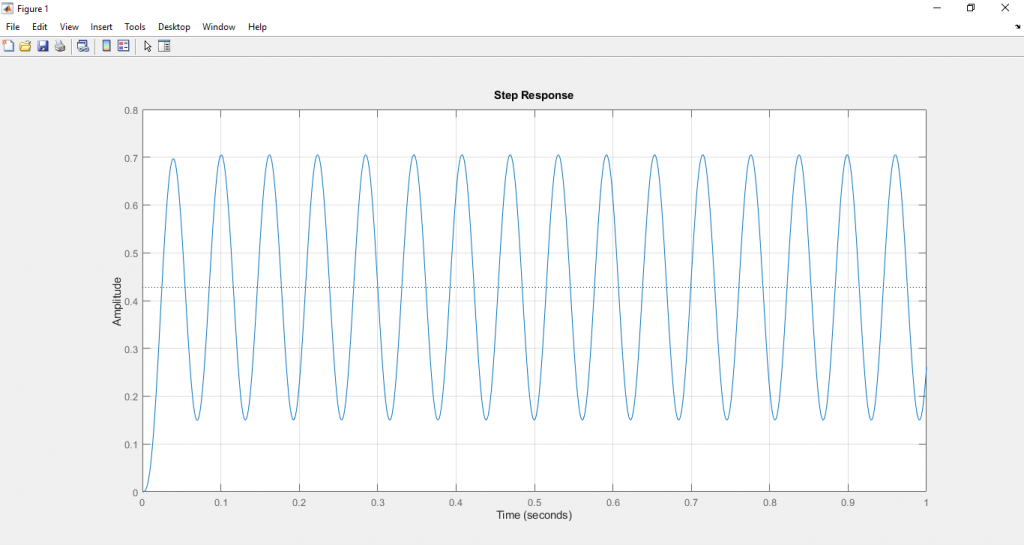
4) คำนวณคาบเวลาที่เกิดการ Oscillation ด้วยการดูจากกราฟ หรือใช้คำสั่งดังนี้
%% Find Tu
[y, t] = step(G, 1);
h = detrend(y);
[~, peaks] = findpeaks(h, 'MinPeakProminence', (max(h)-min(h))/4);
Pcr = mean(diff(t(peaks))) % Oscillation period
5) คำนวณค่าพารามิเตอร์ของพีไอดีคอนโทรลเลอร์โดยตารางที่ 1
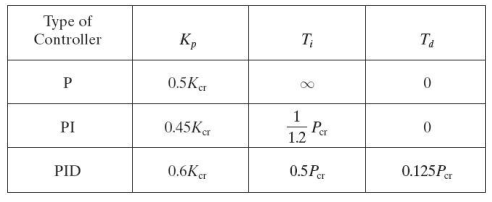
หรือจะใช้คำสั่ง Matlab ดังนี้
%% Classic PID Controller synthesis from Z–N Table
Kp = 0.6*Kcr;
Ti = Pcr/2;
Td = Pcr/8;
Ki = Kp/Ti;
Kd = Kp*Td;
Gc = pid(Kp, Ki, Kd)
%% Closed-loop system step Testing with new PID
Gcl = minreal(feedback(Gc*Gpp, 1))
stepinfo(Gcl)
step(Gcl, 1), grid on
จะได้ผลลัพธ์ดังนี้
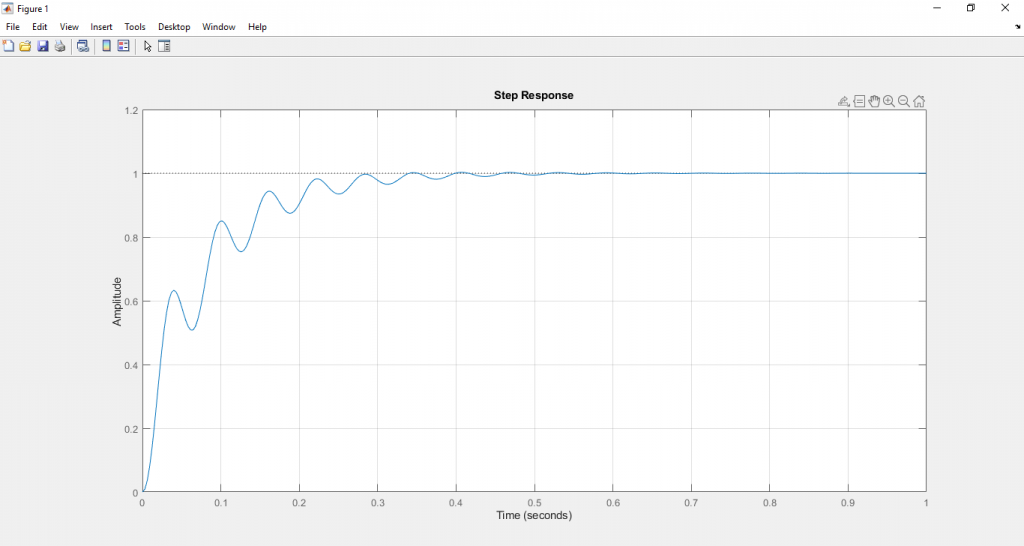
ผู้อ่านสามารถใช้ค่าพารามิเตอร์พีไอดีที่ได้จากขั้นตอนที่ 5 เป็นแนวทางในการ Trial and error เพื่อให้ระบบมีผลตอบสนองที่ดีที่สุดต่อไป
สามารถดาวน์โหลด Matlab Scirpt ได้ที่นี่